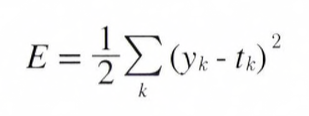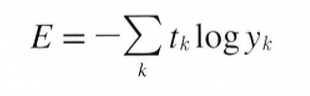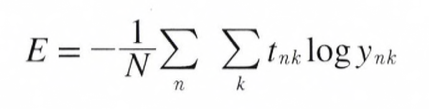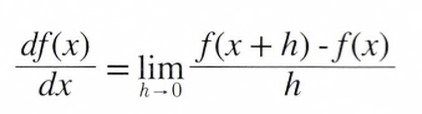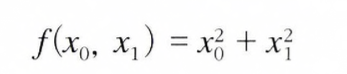이번에는 Neural Network(신경망) 학습에 대하여 설명하고 Pyhon에서 Mnist Dataset의 손글씨 숫자를 학습하는 코드를 구현해 보겠습니다.
Data 주도 학습
Machine Learning(ML)의 중심에는 Data(데이터)가 존재합니다. 데이터가 이끄는 접근 방식 덕에 사람 중심 접근에서 벗어날 수 있습니다.
근데, 보통 문제를 해결하려고 하면 패턴을 찾아내기 위하여 사람은 생각을 하고 결론을 도출합니다.
다만 Machine Learning(기계 학습)에서는 사람의 개입을 최소화하고, 수집한 데이터의 패턴을 찾으려고 시도합니다.
그리고 Neural Network(신경망) & DL(딥러닝)은 기존 Machine Learning(기계 학습)에서 사용하던 방법보다 사람의 개입을 배제할 수 있게 해주는 중요한 특성을 지녔기 때문입니다.
그리고 Machine Learning(기계 학습)에서는 모아진 데이터로부터 규칙을 찾아내는 역할을 '기계'가 담당합니다.
아무것도 없는 상태부터 알고리즘을 설계하는 것보다 효율이 높아 문제를 해결해야 하는 사람의 부담도 덜어줍니다.
다만 이미지를 벡터로 변환할 때 사용하는 특징은 여전히 '사람'이 설계하는것임에 주의해야 합니다.
이 말은 문제에 적합한 특징을 사용하지 않으면 좀처럼 좋은 결과를 얻을 수 없다는 것입니다.
즉, 특징과 기계학습을 활용한 접근에도 문제에 따라서 '사람'이 적절한 특징을 생각해내야 하는것 입니다.
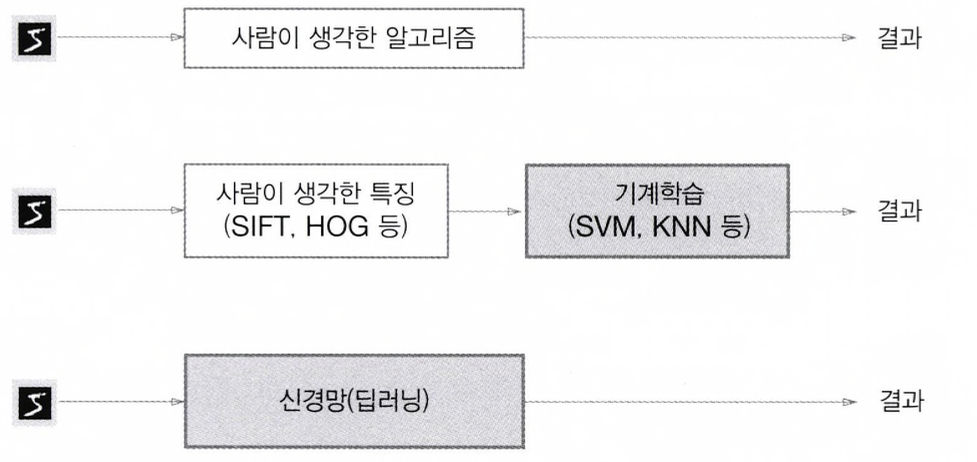
규칙을 '사람'이 만드는 방식에서 '기계'가 데이터로부터 배우는 방식으로의 패러다임 전환: 회색 블록은 사람이 개입하지 않음을 뜻합니다.
위의 그림과 같이 신경망은 이미지를 '있는 그대로' 학습합니다.
그림에서 보이는 2개의 접근 방식(특징, 기계학습 방식)에서는 특징은 사람이 설계 했지만, 신경망은 이미지에 포함된 중요한 특징까지도 '기계'가 스스로 학습할 것입니다.
신경망은 모든 문제를 같은 맥략에서 풀 수 있다는 점에 있습니다. 세부사항과 관계없이 신경망은 주어진 데이터를 온전히 학습하고, 주어진 문제의 패턴을 발견하려 시도합니다.
즉, 신경망은 모든 문제를 주어진 데이터 그대로를 입력 데이터를 활용해 'end-to-end'로 학습할 수 있습니다.
딥러닝을 여기서 종단간 기계학습(end-to-end machine learning)이라고 합니다. 여기서 종단간은 '처음부터 끝까지'라는 의미로 데이터(입력)에서 목표한 결과(출력)를 사람의 개입 없이 얻는다는 뜻입니다.
Training Data(훈련 데이터)와 Test Data(실험 데이터)
기계학습 문제는 데이터를 Training Data(훈련 데이터), Test Data(실험 데이터) 로 나눠 학습과 실험을 수행하는 것이 일반적입니다.
우선 Training Data(훈련 데이터) 만 사용하여 학습하면서 최적의 매개변수를 찾습니다.
그 다음 Test Data(실험 데이터) 를 사용하여 앞서 훈련한 모델의 실력을 평가하는 것입니다.
근데 왜 여기서 Training Data(훈련 데이터), Test Data(실험 데이터) 를 나눠야 할까요?
이유는 우리가 원하는것이 범용적으로 사용하는 모델이기 때문입니다.
이 범용능력을 평가하기 위해서 Training Data(훈련 데이터),Test Data(실험 데이터) 를 분리하는 것입니다.
범용능력
범용능력은 아직 보지 못한 데이터(Training Data(훈련 데이터)에 포함되어 있지 않은 데이터)로 문제를 올바르게 풀어내는 능력입니다.
이 범용 능력을 얻는것이 Machine Learning(기계 학습)의 촤종 목표입니다.
그리고 문제를 올바르게 풀어내려면 데이터셋 하나로만 매개변수의 학습과 평가를 수행하면 올바른 평가가 될 수 없습니다.
수주으이 데이터셋은 제대로 맞히더라도, 다른 데이터셋에는 엉망인 일도 벌어집니다.
만약에 하나의 데이터셋에만 지나치게 최적화된 상태를 Overfitting(오버피팅) 이라고 하는데, 이 오버피팅을 피하거나 방지하는것이 Machine Learning(기계 학습)에서 중요한 과제이기도 합니다.
Loss Function (손실 함수)
Neural Network(신경망) 에서는 '하나의 지표' 를 기준으로 최적의 매개변수 값을 탐색 합니다.
Neural Network(신경망)학습에서 사용하는 지표는 'Loss Function(손실함수)' 이라고 합니다.
'Loss Function(손실함수)' 는 임의의 함수를 사용할 수도 있지만, 일반적으로는 오차제곱합과 Cross-Entropy 오차를 사용합니다.
오차제곱합 (Sum of Squares for Error, SSE)
가장 많이 쓰이는 Loss Function(손실 함수)는 오차제곱합(Sum of Squares for Error, SSE)입니다. 수식으로는 아래의 그림과 같습니다.
오차제곱합 수식
여기서 Yk는 신경망의 출력(신경망이 추정한값), Tk는 정답 lable, k는 데이터의 Dimension(차원)수를 나타냅니다.
한번 원소 10개의 까지 데이터로 예시를 한번 보겠습니다.
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
여기서 이 배열들의 원소는 첫번째 index의 순서대로 숫자 0, 1, 2...일때의 값입니다.
'y' 는 신경망의 출력, 즉, Softmax 함수의 출력입니다. 이는 확률로 해석 할 수 있습니다.
위의 예시에서는 이미지가 '0'일 확률은 0.1, '1'일 확률은 0,05 라고 해석 됩니다.
정답 레이블인 't' 는 정답을 가리키는 위치의 원소 '1' 로 그 외에는 0으로 표기합니다. 또한 숫자 '2' 에 해당하는 원소의 값이 1이므로, 정답이 '2' 임을 알 수 있습니다.
이처럼 한 원소만 1로 하고 그 외에는 0으로 나타내는 표기법을 One-Hot Encoding (원-핫 인코딩) 이라고 합니다.
오차제곱합(Sum of Squares for Error, SSE)은 각 원소의 출력(추정 값) & 정답 label(참 값)의 차를 제곱한 후, 그 총합을 구합니다. 한번 Python 코드로 구현해 보겠습니다.
# y, t는 넘파이 배열
def sum_squares_error(y, t):
return 0.5 * np.sum((y-t)**2)
여기서 인수 y, t는 Numpy Array(넘파이 배열)입니다. 위의 코드는 오차제곱합(Sum of Squares for Error, SSE) 수식을 그대로 수현한 것이니, 설명은 생략하겠습니다. 그러면 이 함수를 한번 사용해 보겠습니다 (by Python Interpreter).
# 정답은 2
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# 예1: '2'일 확률이 가장 높다고 추정함 (0.6)
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> sum_squares_error(np.array(y), np.array(t))
0.0975
# 예2: '7'일 확률이 가장 높다고 추정함 (0.6)
>>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
>>> sum_squares_error(np.array(y), np.array(t))
>>> 0.5975
위의 코드를 보면서 느끼는건 첫번째 추정 결과가 (오차가 더 작으니) 정답에 더 가까울거라고 판단할 수 있습니다.
Cross-Entropy Error, CEE (교차 엔트로피 오차)
또 다른 Loss Function(손실 함수)로서 Cross-Entropy Error, CEE도 자주 이용합니다. 수식은 아래와 같습니다.
Cross-Entropy Error, CEE 수식
여기서 log는 밑이 e인 자연로그(log e) 입니다. Yk는 신경망의 출력, Tk는 정답 레이블 입니다.
또 tk는 정답에 해당하는 인덱스의 원소만 1이고 나머지는 0 입니다. (One-Hot Encoding)
정답 label은 '2'가 정답이라 하고, 이때의 Neural Network(신겸망) 출력이 0.6 이라면, Cross-Entropy Error, CEE (교차 엔트로피 오차)는 -log0.6 = 0.51이 됩니다.
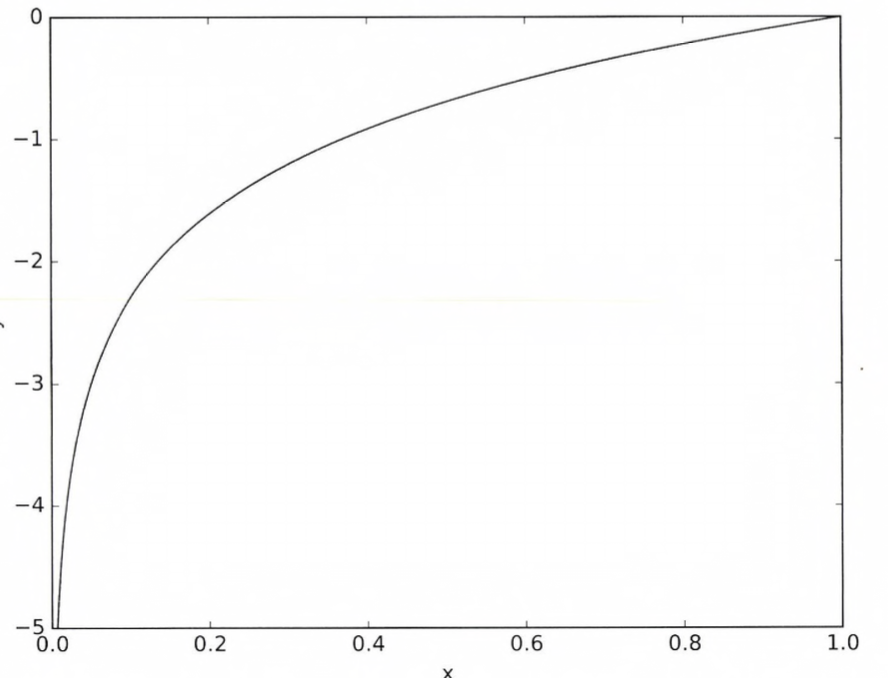
즉, Cross-Entropy Error, CEE (교차 엔트로피 오차)는 정답일 때의 출력이 전체 값을 정하게 됩니다 . 아래의 그래프는 자연로그의 그래프입니다.
자연로그 y = logx의 그래프
위의 식, 그래프와 마찬가지로 x가 1일때 y는 0이 되고, x가 0에 가까워질수록 y의 값은 점점 작아집니다. 반대로 정답일때의 출력이 작아질수록 오차는 커집니다.
그러면 Cross-Entropy Error, CEE (교차 엔트로피 오차)를 한번 코드로 구현해 보겠습니다.
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y+delta))
여기서 y, t는 Numpy Array(넘파이 배열)입니다. 근데, 코드 마지막을 보면 np.log를 계산할 때 아주 작은 값인 delta를 더했습니다 .
이는 np.log() 함수에 0을 입력하면 -inf(마이너스 무한대)가 되어서 계산을 진행할 수 없습니다.
그래서 작은값인 delta를 더해서 절대 0이 되지 않도록 (즉, 마이너스 무한대가 발생하지 않도록)합니다.
그러면 이 cross_entropy_error(y, t) 함수를 써서 간단한 계산을 해봅니다. 정답은 똑같이 '2' 입니다.
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# 예1: 정답일 때의 출력이 0.6인 경우
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> cross_entropy_error(np.array(y), np.array(t))
0.5108
# 예2: 정답일 때의 출력이 0.1인 경우
>>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
>>> cross_entropy_error(np.array(y), np.array(t))
2.3025
예 1: 정답일때의 출력이 0.6인 경우로, 이때의 Cross-Entropy Error는 0.51 입니다.
즉, 결과(오차 값)이 더 낮은 첫번째 추정이 정답일 가능성이 높다고 판단 한 것으로, 앞서 오차제곱합의 판단과 일치합니다.
Mini-Batch Training (미니 배치 학습)
ML(Machine Learning)문제는 Training 데이터를 사용해서 Loss Function(손실 함수)의 값을 구하고, 그 값을 최대한 줄려주는 매개변수를 찾아냅니다.
즉, 이러려면 모든 Training 데이터를 대상으로 손실 함수 값을 구해서 이 모든 손실 함수 값들의 합을 지표로 삼습니다 .
그러면 이제 훈련 데이터 모두에 대한 Loss Function(손실 함수)의 값을 구해보겠습니다.
ex) Cross-Entropy Error,
데이터가 N개라고 하면, 단순히 데이터 하나에 대한 손실 함수를 N개의 데이터로 확장하고 마지막에 N으로 나누어서 정규화 한것입니다.
즉, N으로 나눔으로써 평균 손실 함수를 구한 것입니다. 예를 들어 훈련데이터가 1000개, 10000개든, 상관없이 평균 손실 함수를 구할수 있습니다.
MNIST의 데이터셋은 훈련데이터가 60,000개인데, 모든 데이터를 대상으로 Loss Function(손실 함수)의 합을 구하려면 시간이 오래 걸립니다. 그래서 Training data(훈련 데이터)중 일부만 골라서 학습을 수행 합니다. 이 일부를 Mini-Batch(미니 배치) 라고 합니다.
그리고 이러한 학습 방법을 미니배치 학습(Mini-Batch Training) 이라고 합니다.
그러면 이제 Mini-Batch Training(미니 배치 학습)을 구현하는 코드를 작성해 보겠습니다. (훈련 데이터에서 지정한 수의 데이터를 무작위로 골라냄)
Mini-Batch Training Example Code (by Python)
import sys, os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) = \
load_mnist(normalize=True, one_hot_label=True)
print(x_train.shape) # (60000, 784)
print(t_train.shape) # (60000, 10)
load_mnist: 함수는 Mnist Dataset을 읽어오는 함수입니다.
one_hot_label=True: One-hot Encoding으로 정답 위치의 원소만 1이고, 나머지는 0인 배열을 얻을 수 있음
Input Data(입력 데이터)는 784열 입니다. - (28*28)인 이미지 데이터
정답 label은 10줄 짜리 데이터입니다.
그러면 이 훈련데이터에서 무작위로 10장만 빼내려면 어떻해야 할까요? Numpy의 np.random.choice() 함수를 쓰면 다음과 같이 간단히 해결 할 수 있습니다.
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np,random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
np.random.choice() 지정한 범위 수 중에서 무작위로 원하는 개수만 꺼낼 수 있습니다 .np.random.choice(60000, 10)이면 0이상 60000미만 수중에서 무작위로 10개를 골라냅니다. 아래는 실제로 돌려본 코드입니다.
이 함수가 출력한 배열을 Mini-Batch로 뽑아낼 데이터의 Index로 사용 하면 됩니다.
>>> np.random.choice(60000, 10)
array([8013, 14666, 58210, 23832, 52091, 10153, 8107, 19410, 27260, 21411])Batch 용 Cross-Entropy Error, CEE (교차 엔트로피 오차) 구현하기 (by Python)
Mini-Batch 같은 배치 데이터를 지원하는 Cross-Entropy Error, CEE (교차 엔트로피 오차)는 어떻게 구현할까요?
Cross-Entropy Error, CEE (교차 엔트로피 오차)를 조금만 봐꾸어주면 가능합니다. 아래의 코드는 데이터가 하나인 경우 데이터가 Batch로 묶여서 입력될 경우 모두를 처리할 수 있도록 구현하겠습니다.
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
이 코드에서 y는 신경망의 출력, t는 정답 레이블 입니다.
y가 1차원 이라면? 데이터 하나당 Cross-Entropy Error, CEE (교차 엔트로피 오차)를 구하는 데이터의 형상을 reshape() 함수로 봐꿔줍니다. 그리고 Batch의 크기로 나눠 정규화 하고, 이미지 1장당 평균의 Cross-Entropy Error, CEE (교차 엔트로피 오차)를 계산 합니다.
정답 레이블이 One-Hot Encoding이 아닌, '2', '7' 등의 숫자 레이블로 주어졌을때의 Cross-Entropy Error, CEE (교차 엔트로피 오차) 는 다음과 같이 구현할 수 있습니다.
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
여기서는 One-Hot Encoding 일때 t가 0인 원소는 Cross-Entropy Error, CEE (교차 엔트로피 오차)도 0이므로, 이 계산은 무시해도 됩니다.
다시 말하면 정답에 해당하는 Neural Network(신경망)의 출력만으로 Cross-Entropy Error, CEE (교차 엔트로피 오차)를 계산할 수 있습니다.
그래서 One-Hot Encoding 일때 t, np.log(y)였던 부분을 label로 표현할때 np.log(y[np.arange(batch_size), t])로 구현합니다.
Code 설명
np.arange(batch_size)는 0부터 batch_size-1까지 배열 생성
y[np.arange(batch_size), t]는 각 데이터의 정답 레이블에 해당하는 신경망의 출력을 추출
Loss Function(손실 함수)를 설정하는 이유는?
왜 궅이 Loss Function(손실 함수)를 사용해야 하는 이유는 무엇일까요? 이건 신경망 학습에서 '미분'의 역할을 주목하면 알 수 있습니다.
신경망 학습에서는 최적의 매개변수(가중치, 편향)를 탐색할 때 손실 함수의 값을 가능한 작게 하는 매개변수 값을 찾습니다. 이때 매개변수의 미분(정확히는 Gradient(기울기))를 계산하고, 그 미분값을 단서로 매개변수의 값을 서서이 갱신하는 과정을 반복합니다. 만약의 미분값이 음수면 매개변수의 양의 방향으로 변환 시켜서 Loss Function(손실 함수)의 값을 줄일 수 있지만, 미분값이 양수이면 Weight(가중치) 매개변수를 음의 방향으로 변환시켜 손실함수를 줄일 수 있습니다. 근데 미분값이 0이면? Weight(가중치) 매개변수를 어느쪽으로 움직여도 Loss Function(손실 함수)의 값은 줄어들지 않습니다. 그래서 신경망을 학습할 때 정확도를 지표로 하면 매개변수의 미분이 대부분의 장소에서 0이 되기 때문에 정확도를 지표로 삼아서는 안됩니다.
수치 미분
미분은 한순간의 변화량을 표시한 것입니다. 수식은 아래과 같습니다.
미분 수식
좌변은 f(x)이 x에 대한 미분(x에 대한 f(x)이 변화량) 을 나타내는 기호입니다.
결국 x의 '작은 변화' 가 함수 f(x)를 얼마나 변화시키느냐를 의미 합니다. 이때 시간의 작은 변화, 즉 시간을 뜻하는 h를 한없이 0에 가깝게 한다는 의미를 lim / h->0 으로 나타냅니다.
아래의 코드는 함수를 미분하는 계산을 Python으로 구현했습니다.
def numerical_diff(f, x):
h = 1e-50
return (f(x+h) - f(x)) / h
함수의 이름은 수치 미분(Numerical differentation)에서 따온 numerical_diff(f,x) 로 했습니다.
이 함수는 '함수 f'와 '함수 f에 넘길 인수 x' 두 인수를 받습니다.
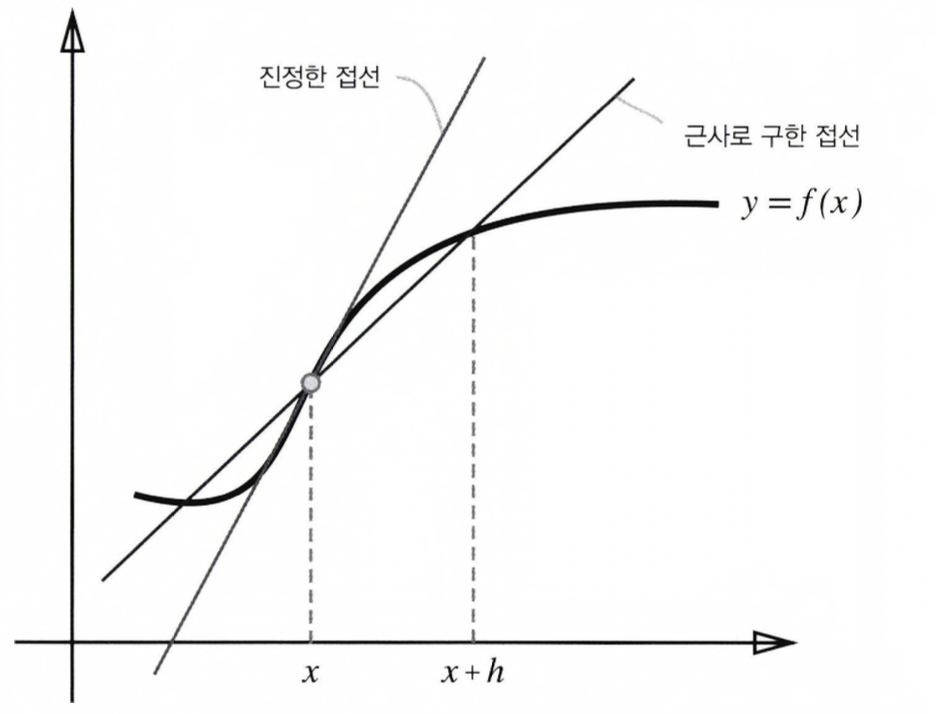
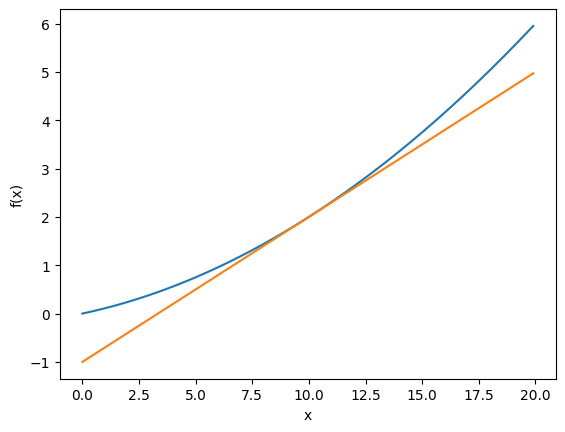
진정한 미분(진정한 접선)과 수치 미분(근사로 구한 접선)의 값은 다르다.
위의 그래프를 보면 수치 미분에는 오차가 포함되빈다. 이 오차를 줄이기 위해서 (x + h)와 (x - h)일 때의 함수 f의 차분을 계산하는 방법을 쓰기도 합니다.
이 차분은 x를 중심으로 그 전후의 차분을 계산한다는 의미에서 중심 차분 혹은 중앙 차분 이라고 합니다.
그러면 그래프를 참고해서 수치 미분을 다시 구현한 코드는 아래와 같습니다.
def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)수치 미분의 예
앞 절의 수치 미분을 사용해서 간단한 함수를 미분해 보겠습니다.
위의 식을 Python으로 구현하면 다음과 같이 됩니다.
def function_1(x):
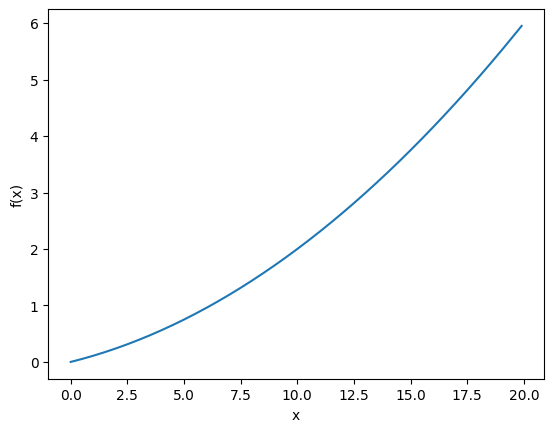
return 0.01*x**2 + 0.1*ximport numpy as np
import matplotlib.pylab as plt
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x, y)
plt.show()위의 수식 그래프, f(x) = 0.01x**2 + 0.1x
그러면 x=5일 때와 10일때 이 함수의 미분을 계산해 보겠습니다.
>>> numerical_diff(function_1, 5)
0.199999
>>> numerical_diff(function_1, 10)
0.299999
이렇게 계산한 미분 값이 x에 대한 f(x)의 변화량, 즉 함수의 기울기 에 해당합니다.
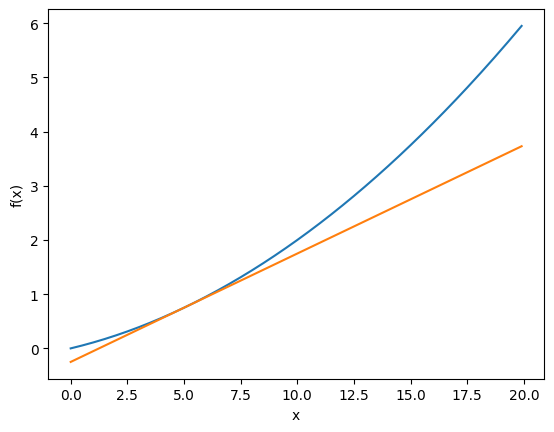
이제 앞에서 구한 수치 미분 값을 기울기로 하는 직선을 그려보겠습니다. 결과는 아래의 그래프와 같게 되어, 함수의 접선에 해당 하는것을 볼 수 있습니다.
좌: x = 5 일때의 접선, 우: x = 10 일때의 접선
편미분
위의 식은 인수들의 제곱 합을 계산하는 단순한 식이지만, 앞과 달리 변수가 2개라는 점에 주의해야 합니다.
이 식은 Python으로 구현 할 수 있습니다.
여기서 인수 x는 numpy 배열 입니다. 각 원소를 제곱하고 그 합을 구하는 간단한 구현입니다.
def function_2(x):
return x[0]**2 + x[1]**2 # 또는 return np.sum(x**2)
f(x0, x1) = x0**2 + x1**2의 그래프
여기서 주의해야 할점은 변수가 2개 입니다. '어느 변수에 대한 미분이냐?' , 즉 x0, x1중 어느 변수에 대한 미분이냐를 구별해야 합니다.
덧붙여 이와 같이 변수가 여럿인 함수에 대한 미분을 편미분
이처럼 편미분 특정 장소의 Gradient(기울기)를 구합니다 .
단, 여러 변수중 목표 변수 하나의 초점을 맞추고 다른 변수는 값을 고정합니다.