My Dev & Engineering Repository

이번에는 Neural Network, 신경망에 데하여 알아보겠습니다.

Neural Network(신경망)은 인공지능, 머신러닝에서 사용되는 컴퓨팅 시스템의 방법중 하나입니다.
인간 또는 동물의 뇌에 있는 생물학적 신경망에서 영감을 받아 설계되었습니다.
생물학적 뉴런이 서로간의 신호를 보내는 방식을 모방합니다.

Perceptron (퍼셉트론)과 Neural Network(신경망)

Perceptron(퍼셉트론)과 Neural Network(신경망)은 공통점이 많습니다. 그래서 다른점을 중점으로 보면서 설명해보겠습니다.

신겸망를 그림으로 나타내면 위의 그림처럼 나옵니다.
맨 왼쪽은 Input Layer(입력층), 중간층은 Hidden layer(은닉층), 오른쪽은 Output Layer(출력층)이라고 합니다.
Hidden layer(은닉층)의 Neuron(뉴런)은 사람 눈에는 보이지 않아서 '은닉' 이라는 표현을 씁니다.
위의 그림에는 입력층 -> 출력층 방향으로 0~2층이라고 합니다. 이유는 Python 배열 Index도 0부터 시작하며, 나중에 구현할 때 짝짓기 편하기 때문입니다.

위의 신겸망은 3개의 Layer(층)으로 구성되지만, Weight(가중치)를 가지는 Layer(층)는 2개여서 '2층 신경망' 이라고 합니다.
* 이 글에서는 실제로 Weight(가중치)를 가지는 Layer(층)의 개수 [Input Layer(입력층), Hidden layer(은닉층), Output Layer(출력층)

이렇게 신경망에 데한 설명을 끝내고, 한번 신경망에서 신호를 어떻게 보내는지 보겠습니다.

Perceptron(퍼셉트론) 복습

Neural Network(신겸망)의 신호 전달 방법을 보기 전에 한번 다시 Perceptron(퍼셉트론)을 보겟습니다.

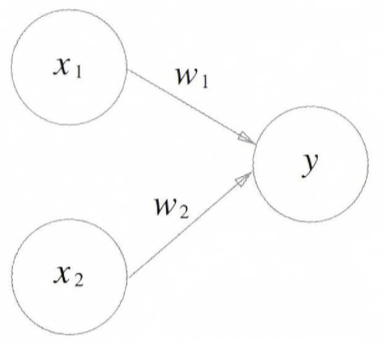
위의 Perceptron(퍼셉트론)은 x1, x2라는 두 신호를 입력받아서 y를 출력하는 Perceptron(퍼셉트론) 입니다.
수식화 하면 아래의 식과 같습니다.

여기서 b는 bias(편향)을 나타내는 parameter(매개변수)이며, Neuron(뉴런)이 얼마나 활성화되느냐를 제어하는 역할을 합니다.
w1, w2는 각 신호의 Weight(가중치)를 나타내는 매개변수로, 각 신호의 영향력을 제어하는 역할을 합니다.
만약에 여기서 bias(편향)을 표시한다면 아래의 그림과 나타낼 수 있습니다.

위의 Perceptron(퍼셉트론)은 Weight(가중치)가 b이고, 입력이 1인 Neuron(뉴런)이 추가되었습니다.
이 Perceptron(퍼셉트론)의 동작은 x1, x2, 1이라는 3개의 신호가 Neuron(뉴런)에 입력되어, 각 신호에 Weight(가중치)를 곱한 후, 다음 Neuron(뉴런)에 전달됩니다.
다음 Neuron(뉴런)에서는 이 신호들의 값을 더하여, 그 합이 0을 넘으면 1을 출력하고, 그렇지 않으면 0을 출력합니다.
참고로, bias(편향)의 input 신호는 항상 1이기 때문에 그림에서는 해당 Neuron(뉴런)은 다른 뉴런의 색을 다르게 하여서 구별했습니다.
위의 Perceptron(퍼셉트론)을 수식화 하면 아래의 식과 같습니다.

위의 왼쪽의 식은 조건 분기의 동작 - 0을 넘으면 1을 출력, 그렇지 않으면 0을 출력하는것을 하나의 함수로 나타내었습니다.
오른쪽의 식은 왼쪽의 수식을 하나의 함수 h(x)라고 하고, 입력 신호의 총합이 함수를 거쳐 반환된후, 그 변환된 값이 y의 출력이 됨을 보여줍니다.
그리고 함수의 입력이 0을 넘으면 1을 출력, 그렇지 않으면 0을 출력합니다. 결과적으로 왼쪽, 오른쪽의 수식이 하는일은 같습니다.

Perceptron(퍼셉트론) 에서의 Activation Function(활성화 함수) 처리과정

전의 h(x)라는 함수를 보셨습니다. 이처럼 입력신호의 총합을 출력 신호로 변환하는 함수를 Activation Function(활성화 함수)라고 합니다.
'활성화 함수' 는 입력신호의 총합이 활성화를 일으키는지를 정하는 역할을 합니다.

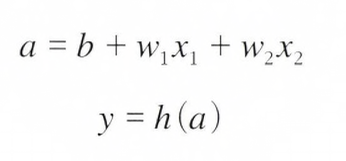
위의 수식은 Weight(가중치)가 곱해진 입력 신호의 총합을 계산하고, 그 합을 Activation Function(활성화 함수)에 입력해 결과를 내는 2단계로 처리됩니다. 그래서 이 식은 2단계의 식으로 나눌 수 있습니다.
위의 수식중의 첫번째 식(위의 식)은 Weight(가중치)가 달린 입력 신호와 Bias(편향)의 총합을 계산한 결과를 'a' 라고 합니다.
그리고 두번째 식(아래의 식)은 Weight(가중치)가 달린 입력 신호와 Bias(편향)의 총합을 계산한 결과인 'a'를 함수 h()에 넣어 y를 출력하는 흐름입니다.

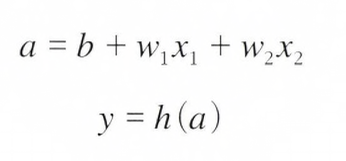
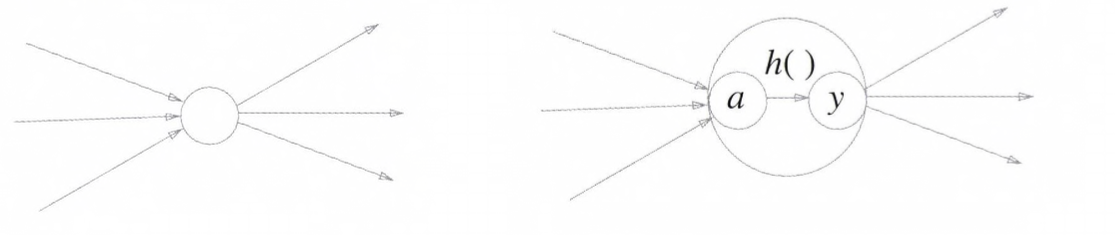
Perceptron(퍼셉트론)에서 Neuron(뉴런)을 큰 원으로 보면 오른쪽의 식(활성화 함수의 수식)은 큰 Neuron(뉴런)안에서의 활성화 함수의 수식을 큰 Neuron(뉴런)안에 처리과정을 시각화 했습니다.
즉, Weight(가중치) 신호를 조합한 결과가 a라는 Node(노드), Activation Function(활성화 함수) h()를 통과하여 y라는 Node(노드)로 변환되는 과정이 나타나 있습니다.

왼쪽은 일반적인 뉴런, 오른쪽은 Activation(활성화) 처리 과정을 명시한 뉴런입니다. (a는 입력 신호의 총합, h()는 활성화 함수, y는 출력)

Activation Function(활성화 함수)

Activation Function(활성화 함수)는 임계값을 기준으로 출력이 봐뀝니다, 이런 함수를 Step Function(계산 함수)라고 합니다.
그래서 Perceptron(퍼셉트론)에서 Activation Function(활성화 함수)로 Step Function(계산 함수)을 이용한다고 합니다.
즉, Activation Function(활성화 함수)으로 쓸수 있는 여러함수중 Step Function(계산 함수)를 사용한다고 하는데, 그러면 Step Function(계산 함수)의외의 다른 함수를 사용하면 어떻게 될까요? 한번 알아보겠습니다.

Sigmoid Function(시그모이드 함수)

Sigmoid Function(시그모이드 함수)는 신경망에서 자주 이용하는 Activation Function(활성화 함수) 입니다.

exp(-x)는 e의 -x승을 뜻하며, e는 자연상수 2.7182....의 값을 가지는 실수입니다.
신경망에서는 Activation Function(활성화 함수)로 Sigmoid 함수를 이용하여 신호를 변환하고, 그 변환된 신호를 다음 뉴런에 전달합니다.
앞에서 본 Perceptron(퍼셉트론) & 앞에서 본 신경망의 주된 차이는 이 Activation Function(활성화 함수) 뿐입니다.
그 외의 Neuron(뉴런)이 여러층으로 이어지는 구조와 신호를 전달하는 방법은 퍼셉트론과 같습니다.

Step Function(계단 함수) 구현하기

이번에는 한번 Step Function(계산 함수)을 한번 구현해 보겠습니다.
입력이 0을 넘으면 1을 출력하고, 그 외에는 0을 출력하는 함수입니다.

def step_function(x):
	if x > 0:
    	return 1
    else:
    	return 0

위의 코드에서는 인수 x는 Float(실수)형만 받아들입니다. 그래서 numpy 배열의 인수는 넣을수가 없습니다.
step_function(np.array([1.0, 2.0]))는 안됩니다. 만약에 numpy 배열도 지원하기 위해서는 아래의 코드처럼 수정할 수 있습니다.

# numpy로 step_function 구현
def step_function(x):
	y = x > 0
    return y.astype(np.int)

아래의 코드는 x라는 Numpy 배열에 부등호 연산을 수행합니다.

>>> import numpy as np
>>> x = np.array([-1.0, 1.0, 2.0)] # Numpy 배열
>>> x
array([-1., 1., 2.])
>>> y = x > 0 # 부등호 연산 수행
>>> y
array([False, True, True], dtype=bool) # data type = bool형

Numpy 배열에 부등호 연산을 수행하면 array 배열의 원소 각각에 부등호 연산을 수행한 bool 배열이 생성됩니다.
여기서 배열 x의 원소 각각이 0보다 크면 True, 0이하면 False로 변환한 새로운 배열 y가 생성됩니다. 여기서 y는 bool 배열입니다.
근데 여기서 우리가 원하는 Step Function(계단 함수)는 0 or 1의 'int형'을 출력하는 함수이므로 배열 y의 원소를 bool -> int형으로 봐꿔줍니다.

>>> y = y.astype(np.int)
>>> y
array([0, 1, 1])

Numpy 배열의 자료형을 변환할 때는 astype() Method를 이용합니다. 원하는 자료형을 인수로 지정하면 됩니다.
또한 Python에서 bool형을 int형으로 변환하면 True는 1로, False는 0으로 변환됩니다.

Step Function(계단 함수)의 그래프

앞에서 정의한 Step Function(계산 함수)를 그래프로 그려보겠습니다. 이때 우리가 지난번에 봤었던 Matplotlib 라이브러리를 사용합니다.

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt


def step_function(x):
    return np.array(x > 0, dtype=np.int64)

X = np.arange(-5.0, 5.0, 0.1)
Y = step_function(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)  # y축의 범위 지정
plt.show()

np.arange(-5.0, 5.0, 0.1)은 -5.0 ~ 5.0까지 0.1간격의 Numpy 배열을 생성합니다. 즉, [-5.0, -4.9 ~ 4.9]를 생성합니다.
Step_function()은 인수로 받은 Numpy 배열의 원소를 각각 인수로 Step function(계산 함수)를 실행하여 그 결과를 다시 배열로 받고, 그후 그래프를 그리면 - plot 결과는 아래의 그림과 같습니다.

위의 그림에서 보면 Step Function - 계단 함수는 0을 경계로 출력이 0에서 1, 또는 1에서 0으로 봐뀝니다.
이렇게 봐뀌는 형태가 계단처럼 보여서 Step Function 이라고 합니다.

Sigmoid Function(시그모이드 함수) 구현하기

한번 Sigmoid Function을 구현해보겠습니다. 한번 Python으로 코드를 한번 만들어 보겠습니다.

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

여기서 np.exp(-x)는 exp(-x) 수식에 해당합니다.
인수가 x가 Numpy 배열이여도 바른 결과가 나온다는 것만 기억해둡니다.

>>> x = np.array([-1.0, 1.0, 2.0])
>>> sigmoid(x)
array([0.26894142, 0.73105858, 0.88079708])

이 함수가 Numpy 배열도 처리할수 있는 이유는 Numpy의 Broadcast 기능에 있습니다.
앞에서 설명 했지만 한번 다시 설명해보겠습니다.

BroadCast (브로드캐스트)

Numpy에서는 형상이 다른 배열끼리도 계산이 가능합니다.
예를 들어서 2 * 2 행렬 A에 Scaler값 10을 곱했습니다. 이때 10이라는 Scaler값이 2 * 2 행렬로 확대된 후 연산이 이뤄집니다.
이러한 기능을 Broadcast (브로드캐스트)라고 합니다.

# Broadcast Example
>>> A = np.array([[1, 2], [3, 4]])
>>> B = np.array([[10, 20]])
>>> A * B
array([[10, 40],
       [30, 80]])

위의 Broadcast의 예시를 보면, 1차원 배열인 B가 2차원 배열인 A와 똑같은 형상으로 변형된 후 원소별 연산이 진행됩니다.

Numpy의 원소 접근

원소의 Index는 0부터 시작합니다. Index로 원소에 접근하는 예시는 아래의 코드와 같습니다.

>>> X = np.array([[51, 55], [14, 19], [0, 4]])
>>> print(X)
[[51 55]
 [14 19]
 [0   4]
>>> X[0] # 0행
array([51, 55])
>>> X[0][1] #(0, 1) 위치의 원소
55

for문으로도 각 원소에 접근할 수 있습니다.

>>> for row in X:
...	    print(row)
...
[51 55]
[14 19]
[0 4]

아니면 Index를 array(배열)로 지정해서 한번에 여러 원소에 접근할 수도 있습니다.
이 기법을 사용하면 특정 조건을 만족하는 원소만 얻을 수 있습니다.

>>> X = X.flatten() #x를 1차원 배열로 변호나(평탄화)
>>> print(X)
[51 55 14 19 0 4]
>>> X[np.array([0, 2, 4])] # 인덱스가 0, 2, 4번째에 있는 원소 얻기
array([51, 14, 0])

아래의 코드는 배열에서 X에서 15 이상인 값만 구할 수 있습니다.

>>> X > 15
array([True, True, False, True, False, False], dtype=bool)
>>> X[X>15]
array([51, 55, 19])

Numpy 배열에 부등호 연산자를 사용한 결과는 bool 배열입니다. (여기서는 X>15)
여기서는 이 bool 배열을 사용해 배열 X에서 True에 해당하는 원소, 즉 값이 15보다 큰 원소만 꺼내고 있습니다.

Sigmoid Function(시그모이드 함수) 그래프 만들어보기

그래프를 그리는 코드는 앞 절의 계단 함수 그리기 코드와 거이 같습니다.
다른 부분은 y를 출력하는 함수를 sigmoid 함수로 변경한 곳입니다.

X = np.arange(-5.0, 5.0, 0.1)
Y = sigmoid(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)
plt.show()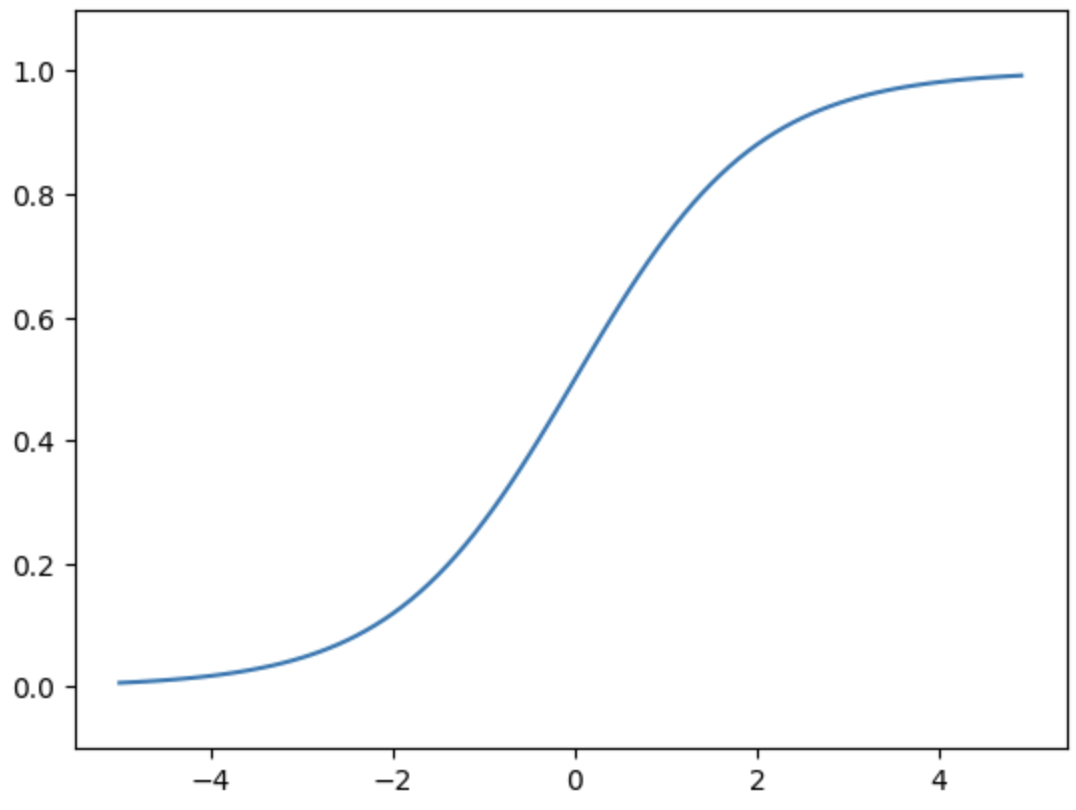

여기서 Step Function(계단 함수), Sigmoid Function(시그모이드 함수)의 차이를 잠깐 설명해보자면
Step Function(계단 함수)는 0, 1 둘중 하나의 값만 돌려주는 반면, Sigmoid Function(시그모이드 함수)는 실수를 돌려준다는 점이 다릅니다.

Summary: Perceptron(퍼셉스톤)에서는 Neuron(뉴런)사이에 0 or 1이 흐르면, Neural Network(신경망)에서는 연속적인 실수가 흐릅니다.

공통점을 보자면, 둘다 입력이 작을때의 출력은 0에 가까워지고 (아니면 0), 입력이 커지면 1에 가까워지는 (아니면 1)이 되는 구조입니다.
즉, Step Function(계단 함수)과 Sigmoid Function(시그모이드 함수)는 입력이 중요하면 큰값, 중요하지 않으면 작은값을 출력하며, 아무리 입력이 작거나 커도, 출력은 0~1 사이입니다.

Non-Linear Function(비선형 함수)

그리고 Step Function(계단 함수)과 Sigmoid Function(시그모이드 함수)의 공통점이 또 있습니다. 둘다 Non-Linear Function(비선형 함수)라는 것입니다.
Non-Linear Function(비선형 함수)는 문자 그대로 '선형이 아닌' 함수 이며, 직선 1개로 그릴수 없는 함수입니다.
신경망에서는 Activation Function(비선형 함수)로 Non-Linear Function(비선형 함수)를 사용해야 합니다.
이유는 Linear Function(선형 함수)를 이용하면 Neural Network(신경망)의 층을 깊게 하는 의미가 없어지기 때문입니다.
- 이유는 Linear Function(선형 함수)의 문제는 층을 아무리 깊게 해도 'Hidden Layer(은닉층)이 없는 네트워크'로도 똑같은 기능을 할 수 있다는데 있습니다. 수식을 한번 보면 선형함수인 h(x) = cx를 활성화 함수로 사용한 3층 네트워크로 예시를 들어보면

y(x) = h(h(h(x))) -> y(x) = c * c * c * x 이렇게 곱셉을 3번 수행하지만 y(x) = ax와 같습니다. a = c의 3승이라고 하면 끝.

이렇게 Hidden Layer(은닉층이 없는 네트워크)가 되기 때문에 선형함수를 이용하면 여러 Layer(층)으로 구성하는 이점을 살릴 수 없습니다.
그래서 Layer(층)를 쌓고 싶으면 Activation Function(활성화 함수)은 Non-Linear Function(비선형 함수)를 사용해야 합니다.

ReLU Function(ReLU 함수)

지금까지 Activation Function(활성화 함수)로서 Step Function(계단 함수)과 Sigmoid Function(시그모이드 함수)를 소개했습니다.
근데, 최근에는 Rectified Linear Unit, ReLU함수를 주로 이용합니다.
ReLU함수는 입력이 0을 넘으면 그 입력을 그대로 출력하고, 0이하면 0을 출력하는 함수입니다.
수식으로는 아래의 식처럼 쓸 수 있습니다.

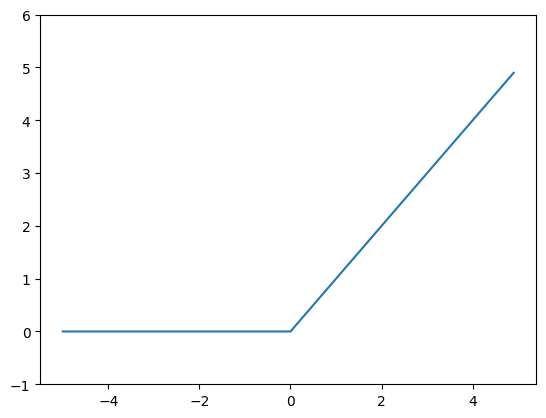
# ReLU함수 시각화 코드

import numpy as np
import matplotlib.pyplot as plt

def relu(x):
    return np.maximum(0, x)  # 입력 x와 0 중 더 큰 값을 반환합니다.

X = np.arange(-5.0, 5.0, 0.1)
Y = ReLU(X)
plt.plot(X, Y)
plt.ylim(-1.0, 6.0)  # y축의 범위를 조정합니다.
plt.show()  # 그래프를 보여줍니다.

위의 코드에서는 Numpy의 Maximum 함수를 사용했습니다. Maximum 함수는 두 입력 중 큰 값을 선택해 반환하는 함수입니다.

다차원 배열의 계산

Numpy의 다차원 배열을 사용한 계산법을 숙달하면 신경망을 효율적으로 구현할 수 있습니다.
다차원 배열도 기본은 '숫자의 집합'입니다. 숫자를 한줄, 직사각형, 3차원으로 늘여놓은것들도 다 다차원 배열이라고 합니다.
한번 1차원 배열을 예시로 한번 보도록 하겠습니다.

1차원 배열 Example Code (by Python)

>>> import numpy as np
>>> A = np.array([1, 2, 3, 4])
>>> print(A)
[1 2 3 4]
>>> np.ndim(A) # 배열의 차원 수 확인
(4, )
>>> A.shape[0]
4

배열의 차원수는 np.ndim() 함수로 확인할 수 있습니다. 또 배열의 형상은 Instance 변수인 shape으로 알 수 있습니다.
위의 예시에서는 A는 1차원 배열이고 원소 4개로 구성되어 있습니다. 근데, A.shape이 튜플을 반환하는것에 주의해야 합니다.
이유는 1차원 배열이라도 다차원 배열일때와 통일된 형태로 결과를 반환하기 때문입니다.
2차원 배열일때의 (4, 3), 3차원 배열일 때는 (4, 3, 2)같은 튜플을 반환합니다.

2차원 배열 Example Code (by Python)

>>> B = np.array([[1,2], [3,4], [5,6]])
>>> print(B)
[[1 2]
 [3 4]
 [5 6]]
>>> np.ndim(B)
2
>>> B.shape
(3, 2)

이번에는 '3 X 2' 배열인 B를 작성했습니다. 3 X 2 배열은 처음 Dimension(차원)에는 원소가 3개, 다음 차원에는 원소가 2개 있습니다.
이때 처음 차원은 0번째 차원, 다음 차원은 1번째 차원에 대응합니다. (Python index는 0부터 시작)
2차원 배열은 특히 행렬 Matrix이라고 부르고 아래의 그림과 같이 배열의 가로 방향을 Row(행), 세로 방향을 Column(열) 이라고 합니다.

행렬의 곱 계산

행렬의 곱을 계산하는 방법은 아래 글에 올라와 있으니까 참고 부탁드립니다!

[DL] Numpy & 행렬에 데하여 알아보기

Numpy가 뭐에요? Python 에서 과학적 계산 & 수치를 계산하기 위한 핵심 라이브러리입니다. NumPy는 고성능의 다차원 배열 객체와 이를 다룰 도구를 제공합니다. 수치 계산을 위한 매우 효과적인 인터

daehyun-bigbread.tistory.com

신경망에서의 행렬 곱

Numpy 행렬을 써서 행렬의 곱으로 신경망을 한번 구현해 보겠습니다. 아래의 그림처럼 간단한 신경망을 구성해 보겠습니다.

이 구현에서도 X, W, Y의 형상을 주의해서 봐야합니다.
특히 X, W의 대응하는 차원의 원소 수가 같아야 한다는 걸 잊지 말아야 합니다.

>>> X = np.array([1, 2])
>>> X.shape
(2,)
>>> W = np.array([[1, 3, 5], [2, 4, 6]])
>>> print(W)
[[1 3 5]
 [2 4 6]]
>>> W.shape
(2, 3)
>>> Y = np.dot(X, W)
>>> print(Y)
[5 11 17]

다차원 배열의 Scaler곱을 곱해주는 np.dot 함수를 사용하면 이처럼 단번에 결과 Y를 계산 할 수 있습니다. Y의 개수가 100개든, 1000개든...
만약에 np.dot을 사용하지 않으면 Y의 원소를 하나씩 따져봐야 합니다. 아니면 for문을 사용해서 계산해야 하는데 귀찮습니다..
그래서 행렬의 곱으로 한꺼번에 계산해주는 기능은 신경망을 구현할 때 매우 중요하다고 말할 수 있습니다.

3-Layer Neural Network(3층 신경망) 구현하기

이번에는 3층 신경망에서 수행되는 입력부터 출력까지의 처리(순방향 처리)를 구현하겠습니다.
그럴려면 Numpy & 다차원 배열을 사용해야 합니다. 여기서 Numpy 배열을 잘 쓰면 적은 코드로 신경망의 순방향 처리를 완성할 수 있습니다.

3층 신경망: 입력층(0층)은 2개, 첫번째 은닉층(1층)은 3개, 두번째 은닉층(2층)은 2개, 출력층(3층)은 2개의 뉴런으로 구성된다.

신경망에서의 표기법

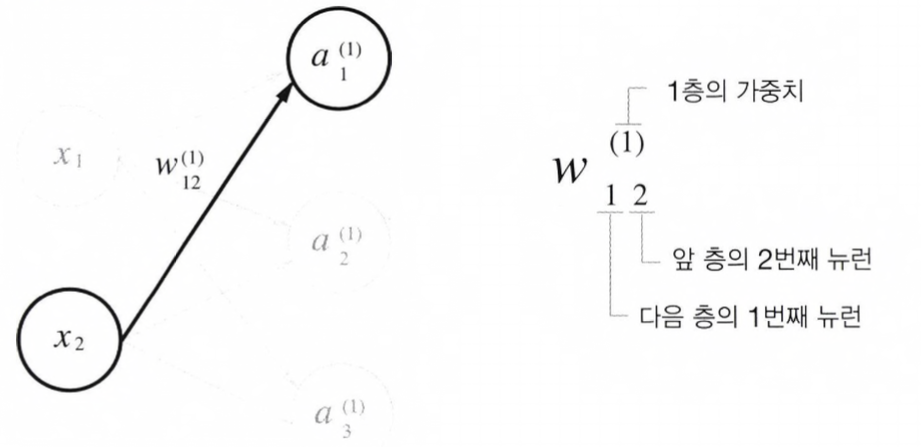
Weight(가중치)와 Hidden Layer(은닉층) Neuron의 오른쪽 위에는 '(1)' 이 붙어있습니다.
이는 1층의 Weight(가중치), 1층의 Neuron(뉴런)을 의미하는 번호입니다.
또한 Weight(가중치)의 오른쪽 아래의 두 숫자는 다음층의 "Neuron(뉴런)-다음층 번호, 앞층 Neuron(뉴런)의 Index 숫자-앞층 번호" 입니다.

각 Layer(층)의 신호 전달 구현하기

Input Layer(입력층) -> 1층

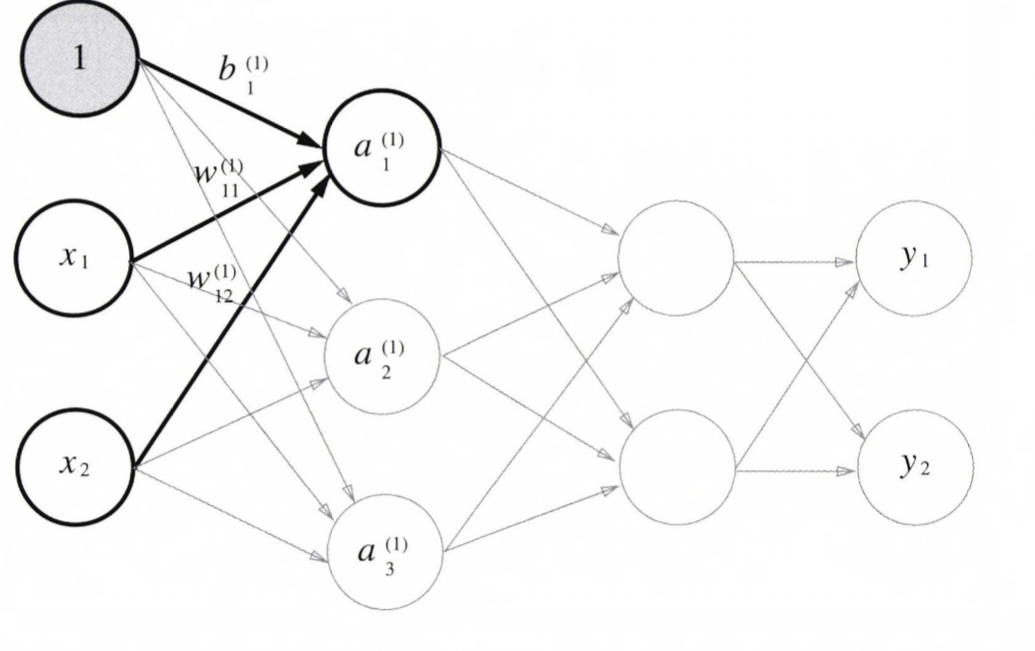
위의 그림에는 Bias(편향)을 의미하는 Neuron(뉴런)인 1이 추가되었습니다. 그리고 Bias(편향)은 오른쪽 아래 Index가 하나밖에 업다는것에 주의하세요. 이는 앞 층의 편향 뉴런(1)이 하나뿐이기 때문입니다.
그러면 이제 알고있는 사실들을 반영하여 수식으로 나타내고, 간소화 해보겠습니다.

왼: 수식, 오: 행렬의 곱을 이용하여 1층의 'Weight(가중치)'부분 간소화

Weight(가중치)부분을 간소화 했을때, 행렬 A, X, B, W는 각각 다음과 같습니다.

그러면 이제 Numpy의 다차원 배열을 사용해서 코드로 구현해 보겠습니다.

# 입력 신호, 가중치, 편향은 적당한 값으로 설정
X = np.array([1.0, 0.5])
W1 = np.array([0.1, 0.3, 0.5], [0.2, 0.4, 0.6])
B1 = np.array([0.1, 0.2, 0.3])

print(W1.shape) # (2,3)
print(X.shape) # (2,)
print(B1.shape) # (3,)

A1 = np.dot(X, W1) + B1

이 계산은 W1은 2 * 3 행렬, X는 원소가 2개인 1차원 배열입니다. 여기서도 W1과 X에 대응하는 차원의 원소 수가 일치하고 있습니다.

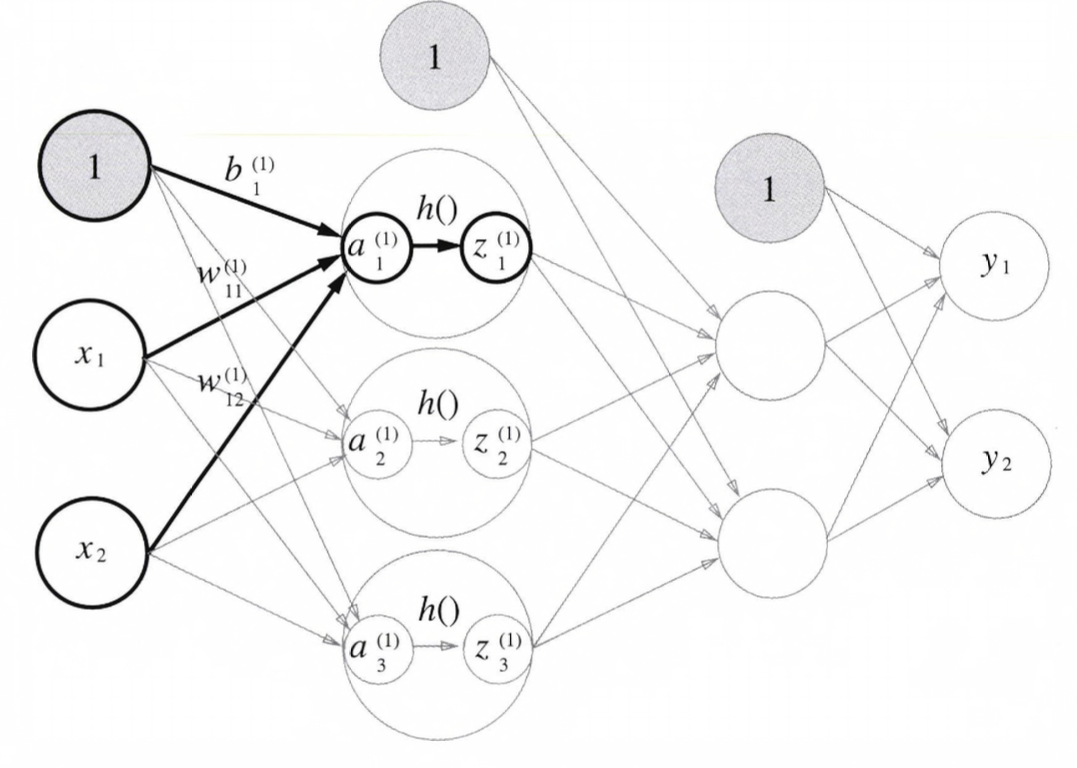
Hidden Layer에서의 Weight(가중치)의 합(가중 신호 + 편향)을 a로 표기하고 Activation Function(활성화 함수) h()로 변환된 신로를 z로 표기합니다.
여기선 Activation Function(활성화 함수)을 Sigmoid 함수를 사용합니다.

Input Layer(입력층) -> 1층 Python Code Example

Z1 = sigmoid(A1)

print(A1) # [0.3, 0.7, 1.1]
print(Z1) # [0.57444252, 0.66818777, 0.75026011]

1층 (Hidden Layer) -> 2층 (Hidden Layer)

여기서는 1층의 Hidden Layer의 출력 Z1이 2층의 Hidden Layer의 Input이 된다는점만 제외하면 앞의서의 구현과 같습니다.
이렇게 Numpy 배열을 사용하면 Layer(층) 사이의 신호 전달을 쉽게 구현할 수 있습니다.

1층 (Hidden Layer) -> 2층 (Hidden Layer) Python Code Example

W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])

print(Z1.shape) # (3,)
print(W2.shape) # (3,2)
print(B2.shape) # (2,)

A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)

2층 (Hidden Layer) -> 출력층 (Output Layer)

여기서 항등 함수 identify_function()을 정의하고, 이를 Output Layer(출력층)의 Activation Function(활성화 함수)로 이용했습니다.
항등 함수는 Input(입력)을 그대로 출력하는 함수입니다. 위의 예시에서는 그대로 identify_function()을 굳이 정의할 필요는 없지만, 흐름을 통일하기 위해서 이렇게 구현했습니다.
그리고 Output Layer(출력층)의 Activation Function(활성화 함수)는 '시그마' σ()로 표시해서 Hidden Layer(은닉층)의 Activation Function(활성화 함수) h()와는 다름을 명시했습니다.

2층 (Hidden Layer) -> 출력층 (Output Layer) Python Code Example

def identity_function(x):
	return x
    
W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])

A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3)

구현 정리

이제 3층 신경망에 데한 설명은 끝내고, 지금까지 구현한 내용을 정리해 보겠습니다.
신경망 구현의 관례에 따라 Weight(가중치) W1만 대문자로 쓰고, 그 외 Bias(편향)과 중간 결과 등은 모두 소문자로 썼습니다.

def init_network():
	network = {}
    network['W1'] = np.array([0.1, 0.3, 0.5], [0.2, 0.4, 0.6])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])
    
    return network
    
def forward(network, x):
	W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(x, W2) + b2
    z2 = sigmoid(a1)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)
    
    return y
    
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)

여기서 Init_network()와 forward()라는 함수를 정의하였습니다.
Init_network() 함수는 Weight(가중치)와 Bias(편향)을 초기화 하고, 이들을 Dictionary 변수인 network에 저장합니다.
이 Dictionary 변수 network는 각 Layer(층)에 필요한 매개변수(Weight & Bias)를 모두 저장합니다.
forward() 함수는 입력 신호를 출력으로 변환하는 처리 과정을 모두 구현합니다.
또한 함수 이름을 forward() 라고 한건 신호가 순방향 (입력->출력)으로 전달됨(순전파)임을 알리기 위함입니다.

Output Layer(출력층) 설계하기

Neural Network(신경망)은 Classification(분류), Regression(회귀)에 모두 이용할 수 있습니다.

다만, 둘 중 어떤 문제냐에 따라서 Output Layer(출력층)에서 사용하는 Activation Function(활성화 함수)이 달라집니다.
일반적으로 Regression(회귀)에는 항등함수를, Classification(분류)에는 Softmax 함수를 사용합니다.

Identify(항등) 함수 & Softmax 함수 구현하기

Identify Function(항등함수)은 입력을 그대로 출력합니다.
입력, 출력이 항상 같다는 뜻의 항등입니다. 그래서 Output Layer(출력층)에서 Identify Function(항등 함수)를 사용하면 입력 신호가 그대로 출력 신호가 됩니다.
항등 함수의 처리는 신경망 그림으로 아래의 그림처럼 됩니다. 또한 Identify Function(항등 함수)에 의한 변환은 Hidden Layer(은닉층)에서의 Activation Function(활성화 함수)와 마찬가지로 화살표로 그립니다.

Classification(분류)에서 사용하는 Softmax Function(소프트맥스 함수)의 식은 다음과 같습니다.

여기서 exp(x)는 e의 x승을 뜻하는 Exponential Function(지수 함수)입니다. (여기서 e는 자연상수 입니다)
n은 출력층의 뉴런 수, yk는 그중 k번째 출력임을 뜻합니다.
Softmax 함수의 분자는 입력 신호 ak의 지수함수, 분모는 모든 입력 신호의 지수 함수의 합으로 구성됩니다.
Softmax의 출력은 모든 입력 신호로부터 화살표를 받습니다. 위의 수식의 분모에서 보면, 출력층의 각 뉴런이 모든 입력 신호에서 영향을 받기 때문입니다.

그러면, 한번 Softmax 함수를 한번 구현해 보겠습니다.

>>> a = np.array([0.3, 2.9, 4.0])
>>> exp_a = np.exp(a) # 지수 함수
[ 1.34985881 18.17414537 54.59815003]

>>> sum_exp_a = np.sum(exp_a) # 지수 함수의 합
>>> print(sum_exp_a_
74.1221152102

>>> y = exp_a / sum_exp_a
>>> print(y)
[ 0.01821127 0.24519181 0.73659691 ]

이번에는 이 흐름을 Python 함수로 정의해보겠습니다.

def softmax(a):
	exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    
    return y

Softmax 함수 구현시 주의점

softmax() 함수는 컴퓨터로 계산할 때 결함이 있습니다. Overflow 문제가 있습니다.
softmax() 함수는 지수 함수를 사용하는데, 지수 함수란 것이 아주 큰 값을 뱉습니다. e의 10승은 20,000이 넘고, e의 100승은 0이 40개가 넘는 큰 값이 되고, 만약 e의 1000승이 되면 무한대를 의미하는 inf가 됩니다.
이런 큰 값을 나눗셈을 하면 결과 수치가 '불안정' 해집니다.
이 문제를 해결하기 위해서 Softmax 함수를 개선해 보겠습니다.

C라는 의미의 정수를 분자와 분모 양쪽에 곱했습니다. 그 다음으로 C를 지수 함수 exp()안으로 옮겨서 logC로 만듭니다.
그리고 logC를 새로운 기호 C로 봐꿉니다.
여기서 말하는 것은 Softmax의 지수 함수를 계산할 때 어떤 정수를 더해도 결과는 봐뀌지 않습니다.
그리고 일반적으로 입력 신호중 최대값을 이용하는것이 일반적입니다.

>>> = np. array([ 1010, 1000, 990])
>>> np.exp(a) / np.sum(np.exp(a)) # softmax 함수의 계산
array([ nan, nan, nan]) # 제대로 계산이 되지 않는다.
>>>
>>> c = np.max(a) #c = 1010 (최대값)
>>> a - c
array([ 0, - 10, - 20 ])
>>>
>>> np.exp(a-c) / np.sum(np.exp(a-c))
array([ 9.99954600e - 01, 4.53978686e - 05, 2.06106005e - 09])

여기서 보는것 처럼 아무런 조치 없이 그냥 계산하면 nan이 출력됩니다. (nan은 not a number의 약자입니다.)
하지만 입력 신호중 최대값(이 예에서는 c)를 빼주면 올바르게 계산할 수 있습니다. 이 내용에 기반해서 다시 구현하면 아래의 함수와 같습니다.

def softmax(a):
	c = np.max(a)
    exp_a = np.exp(a-c) # 오버플로 대책
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    
    return y

Softmax 함수의 특징

softmax() 함수를 사용하면 신겸망의 출력은 다음과 같이 계산할 수 있습니다.

>>> a = np.array([0.3, 2.9, 4.0])
>>> y = softmax(a)
>>> print(y)
[0.01821127, 0.24519181, 0.73659691]
>>> np.sum(y)
1.0

Softmax 함수의 출력은 0 ~ 1.0 사이의 실수입니다. 그리고 함수 출력의 총합은 1입니다.
출력 총합이 1이 된다는건 Softmax 함수의 중요한 성질이며, 이 성질 덕분의 Softmax 함수의 출력은 '확률'로 해석할 수 있습니다.
확률로 해석할 수도 있는데 y[0]의 확률은 1.8%, y[1]의 확률은 24.5%, y[2]의 확률은 73.7%로 해석할 수 있습니다.
여기서 2번째 원소의 확률이 가장 높으니 답은 2번째 클래스라고 할 수 있습니다.
즉, Softmax 함수를 이용해서 문제를 확률(통계)적으로 대응할 수 있습니다.

Output Layer(출력층)의 Neuron(뉴런) 수 정하기

Output Layer(출력층)의 Neuron(뉴런)수는 풀려는 문제에 맞게 적절히 정해야 합니다.
보통 클래스에 수에 맞게 설정하는 것이 일반적입니다. 입력이미지를 숫자 0~9중 하나로 분류하는 문제면 Output Layer(출력층)의 뉴런을 10개로 설정합니다.

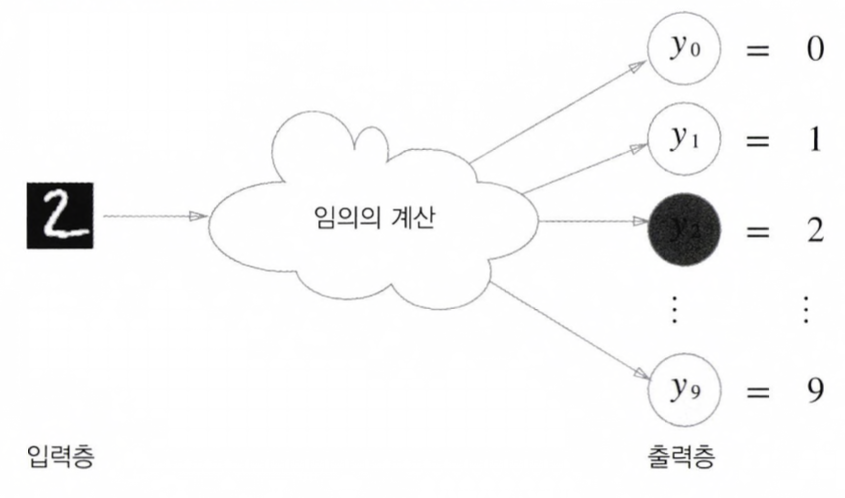
위에서 부터 출력층 뉴런은 차례로 숫자 0~9 까지 대응하며, 뉴런의 회색 농도가 해당 뉴런의 출력 값의 크기를 의미합니다.
여기서는 색이 가장 깉은 y2 뉴런이 가장 큰 값을 출력합니다. 그래서 이 신경망에서는 y2, 입력 이미지의 숫자 '2'로 판단했습니다.

Example - Mnist Dataset

지금까지 알아본 신경망에 데한 예시를 적용해 보겠습니다. 바로 Mnist 라고 하는 손글씨 숫자 분류입니다.

여기서는 이미 학습된 매개변수를 사용하여 학습 과정은 생략라고, 추론 과정만 구현합니다.
여기서 이 추론 과정을 신경망의 Forward Propagation(순전파)라고 합니다.
Mnist Datasdet은 0~9 까지의 숫자 이미지로 구성되어 있으며, Training Image가 60,000장, Test Image가 10,000장이 있습니다.
이 훈련 이미지를 사용하여 모델을 학습하고, 학습한 모델로 실험 이미지를 얼마나 정확하게 분류하는지를 평가합니다.

Mnist의 이미지 데이터는 28 * 28의 회색조 이미지 (1채널)이며, 각 픽셀은 0에서 255까지의 값을 취합니다.
또한 각 이미지에는 7, 2, 1, 3, 5와 같이 그 이미지가 셀제 의미하는 숫자가 label로 붙어 있습니다.
load_minst 함수는 읽은 MNIST 데이터를 "(훈련이미지, 훈련레이블), (실험이미지, 실험레이블)" 형식으로 반환합니다.
인수로는 normalize, flatten, one_hot_label 3개가 있는데 세인수 모두 bool값입니다.
- normalize는 이미지의 픽셀 값을 0.0~1.0 사이의 값으로 정규화 할지를 정합니다. False면 입력 이미지의 픽셀 값은 0~255사이의 원래값을 유지합니다.
- flatten은 입력 이미지를 1차원 배열로 만들지를 정하며, False로 하면 1 * 28 * 28, 3차원 배열, True로 하면 784개의 원소로 이루어진 1차원 배열로 저장합니다. (28 * 28 = 784)
- one_hot_label은 label을 one_hot_encoding 형태로 저장할지를 정합니다.
  - 예시를 간단하게 들어보면 [0,0,0,0,1,0,0] 이러면 정답을 뜻하는 원소는 '1'이고 나머지는 '0'인 배열입니다.
  - 만약 label이 False면 '7', '2'같이 숫자 형태의 label을 저장하고, True이면 label을 one_hot_encoding하여 저장합니다.

import sys
import os
import pickle
import numpy as np
sys.path.append(os.pardir)  # 부모 디렉터리의 파일을 가져올 수 있도록 설정
from dataset.mnist import load_mnist
from PIL import Image

def img_show(img):
	pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()
    
(x_train, t_train), (x_test, t_test) = \
	load_mnist(flatten=True, normalize=False)

img = x_train[0]
label = t_train[0]
print(label) # 5

print(img.shape) # (784,)
img = img.reshape(28, 28) # 원래 이미지의 모양으로 변형
print(img.shape) # (28, 28)

img_show(img)

이 코드에서 알아야하는건 flatten=True로 설정해 읽어 들인 이미지는 1차원 넘파이 배열로 저장되어 있습니다.
그래서 이미지를 표시할 때는 원래 형상인 28 * 28 크기로 변형해야 합니다. 이때, reshape() Method에 원하는 형상을 인수로 지정하면 넘파이 배열의 형상을 봐꿀수 있습니다.
그리고 Numpy로 저장된 이미지 데이터를 PIL용 데이터 객체로 변환해야 하며, 이미지 변환은 Image.fromarray() 함수가 수행합니다.

신경망의 추론 처리

여기서 Input Layer Neuron(입력층 뉴런)을 784개, Output Layer Neuron(출력층 뉴런)을 10개로 구성합니다.
입력층 뉴런의 개수가 784개인 이뉴는 이미지 크기가 28*28=784이기 때문이고, 출력층 뉴런이 10개인 이유는 0에서 9까지의 숫자를 구분하는 문제이기 때문입니다.
Hidden Layer(은닉층)은 2개로, 첫번째는 50개, 두번째는 100개의 뉴런을 배치합니다.

def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=True, one_hot_label=False)
    return x_test, t_test


def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        # 학습된 가중치 매개변수가 담긴 파일
        # 학습 없이 바로 추론을 수행
        network = pickle.load(f)

    return network


def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y

init_network() 함수에서는 pickle 파일인 sample_weight.pkl에 저장된 '학습된 가중치 매개변수'파일을 읽습니다.
이 파일 안에는 Weight(가중치), Bias(편향) 매개변수가 Dictionary 변수로 저장되어 있습니다.

x, t = get_data()
network = init_network()
accuracy_cnt = 0

for i in range(len(x)):
    y = predict(network, x[i])
    p = np.argmax(y)  # 확률이 가장 높은 원소의 인덱스를 얻는다.
    if p == t[i]:
        accuracy_cnt += 1

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))  # Accuracy: 0.9352

위의 코드는 정확도를 판단하는 코드입니다.
반복문을 돌면서 x에 저장된 이미지 데이터를 1장씩 꺼내서 predict() 함수로 분류하고, 각 label의 확률을 numpy 배열로 변환합니다.
그리고 np.argmax() 함수로 이 배열에서 가장 큰(확률값이 제일 높은) 원소의 index를 구합니다.
그리고 신경망이 predict(예측)한 답변과 정답 label을 비교하여 맞힌 숫자(accuracy_cnt)를 세고, 이를 전체 이미지 숫자로 나눠 정확도를 구합니다.

배치 처리

위의 그림을 보며느 원소 784개로 구성된 1차원 배열 (원래는 28 * 28인 2차원 배열)이 입력되어 마지막에는 원소가 10개인 1차원 배열이 출력되는 흐름입니다. 이는 이미지 데이터를 1장만 입력했을 때의 흐름입니다.
그러면 만약에 이미지를 여러개를 한꺼번에 입력하는 경우는 어떻게 될까요? 이미지 100개를 묶어서 predict() 함수에 한번에 넘깁니다. x의 형상을 100 * 784로 봐꿔서 100장 분량의 데이터를 하나의 입력 데이터로 표현하면 됩니다. 아래의 그림처럼 됩니다.

위의 그림과 같이 입력 데이터의 형상은 100 * 784, 출력 데이터의 형상은 100 * 10 입니다.
이는 100장 분량 입력 데이터의 결과가 한 번에 출력됨을 나타냅니다. x[0], y[0]에 있는 0번째 이미지와 그 추론결과가 x[1]과 y[1]에는 1번째의 이미지와 그 결과가 저장되는 식입니다.
이렇게 하나로 묶은 입력 데이터를 Batch(배치)라고 합니다.

x, t = get_data()
network = init_network()

batch_size = 100 # 배치 크기
accuracy_cnt = 0

for i in range(0, len(x), batch_size):
    x_batch = x[i:i+batch_size]
    y_batch = predict(network, x_batch)
    p = np.argmax(y_batch, axis=1)
    accuracy_cnt += np.sum(p == t[i:i+batch_size])

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))  # Accuracy:0.9352

위에서 range() 함수는 (start, end)처럼 인수를 2개 지정해서 호출하면 start에서 end-1 까지의 정수를 차례로 반환하는 Iterator(반복자)를 돌려줍니다.
또 range(start, end, step)처럼 인수를 3개 지정하면 start에서 end-1 까지 step 간격으로 증가하는 정수를 반환하는 반복자를 돌려줍니다.
이 range() 함수가 반복하는 반복자를 바탕으로 x[i:i+batch_size]에서 입력 데이터를 묶습니다.
x[i:i+batch_size]은 입력 데이터의 i번째 부터 i+batch_size번째의 데이터를 묶는다는 의미입니다.
여기서는 batch_size가 100이므로 x[0:100], x[100:200] 처럼 앞에서 부터 100장씩 묶어 꺼내게 됩니다.
그리고 argmax()는 최대값의 index를 가져옵니다.
마지막으로 '==' 연산자를 이용해서 Numpy 배열과 비교하여 True, False로 구성된 Bool 배열로 만들고, 이 결과 배열에서 True가 몇개인지 샙니다.

Summary

- 신경망에서 활성화 함수로 시그모이드 함수, ReLU 함수 같이 매끄럽게 변화하는 함수를 이용한다.
- Numpy의 다차원 배열을 잘 사용하면 신경망을 효율적으로 구현할 수 있다.
- Maching Learning 문제는 크게 회귀와 분류로 나눌수 있다.
- 출력층의 활성화 함수 - 회귀에서는 주로 항등 함수, 분류에서는 Softmax 함수를 이용한다.
- 분류에서는 출력츠으이 뉴런 수를 분류하려는 클래스 수와 같게 설정한다.
- 입력 데이터를 묶은 것을 배치라고 하며, 추론 처리를 이 배치 단위로 진행하면 결과를 훨씬 빠르게 얻을 수 있다.

저작자표시 비영리 동일조건

'🖥️ Deep Learning' 카테고리의 다른 글

[DL] Gradient (기울기), Training Algorithm(학습 알고리즘) (0)	2024.03.23
[DL] Neural Network Training (신경망 학습) (0)	2024.03.21
[DL] Perceptron (퍼셉트론) (0)	2024.03.12
[DL] Matplotlib 라이브러리에 데하여 알아보기 (0)	2024.03.05
[DL] Gradient Vanishing, Exploding - 기울기 소실, 폭팔 (0)	2024.01.26

Notice

Perceptron (퍼셉트론)과 Neural Network(신경망)

Perceptron(퍼셉트론) 복습

Perceptron(퍼셉트론) 에서의 Activation Function(활성화 함수) 처리과정

Activation Function(활성화 함수)

Sigmoid Function(시그모이드 함수)

Step Function(계단 함수) 구현하기

Step Function(계단 함수)의 그래프

Sigmoid Function(시그모이드 함수) 구현하기

BroadCast (브로드캐스트)

Numpy의 원소 접근

Sigmoid Function(시그모이드 함수) 그래프 만들어보기

Non-Linear Function(비선형 함수)

ReLU Function(ReLU 함수)

다차원 배열의 계산

1차원 배열 Example Code (by Python)

2차원 배열 Example Code (by Python)

행렬의 곱 계산

신경망에서의 행렬 곱

3-Layer Neural Network(3층 신경망) 구현하기

신경망에서의 표기법

각 Layer(층)의 신호 전달 구현하기

Input Layer(입력층) -> 1층

Input Layer(입력층) -> 1층 Python Code Example

1층 (Hidden Layer) -> 2층 (Hidden Layer)

1층 (Hidden Layer) -> 2층 (Hidden Layer) Python Code Example

2층 (Hidden Layer) -> 출력층 (Output Layer)

2층 (Hidden Layer) -> 출력층 (Output Layer) Python Code Example

구현 정리

Output Layer(출력층) 설계하기

Identify(항등) 함수 & Softmax 함수 구현하기

Softmax 함수 구현시 주의점

Softmax 함수의 특징

Output Layer(출력층)의 Neuron(뉴런) 수 정하기

Example - Mnist Dataset

신경망의 추론 처리

배치 처리

Summary

'🖥️ Deep Learning' 카테고리의 다른 글

티스토리툴바

SUBSCRIBE

Notice

Perceptron (퍼셉트론)과 Neural Network(신경망)

Perceptron(퍼셉트론) 복습

Perceptron(퍼셉트론) 에서의 Activation Function(활성화 함수) 처리과정

Activation Function(활성화 함수)

Sigmoid Function(시그모이드 함수)

Step Function(계단 함수) 구현하기

Step Function(계단 함수)의 그래프

Sigmoid Function(시그모이드 함수) 구현하기

BroadCast (브로드캐스트)

Numpy의 원소 접근

Sigmoid Function(시그모이드 함수) 그래프 만들어보기

Non-Linear Function(비선형 함수)

ReLU Function(ReLU 함수)

다차원 배열의 계산

1차원 배열 Example Code (by Python)

2차원 배열 Example Code (by Python)

행렬의 곱 계산

신경망에서의 행렬 곱

3-Layer Neural Network(3층 신경망) 구현하기

신경망에서의 표기법

각 Layer(층)의 신호 전달 구현하기

Input Layer(입력층) -> 1층

Input Layer(입력층) -> 1층 Python Code Example

1층 (Hidden Layer) -> 2층 (Hidden Layer)

1층 (Hidden Layer) -> 2층 (Hidden Layer) Python Code Example

2층 (Hidden Layer) -> 출력층 (Output Layer)

2층 (Hidden Layer) -> 출력층 (Output Layer) Python Code Example

구현 정리

Output Layer(출력층) 설계하기

Identify(항등) 함수 & Softmax 함수 구현하기

Softmax 함수 구현시 주의점

Softmax 함수의 특징

Output Layer(출력층)의 Neuron(뉴런) 수 정하기

Example - Mnist Dataset

신경망의 추론 처리

배치 처리

Summary

'🖥️ Deep Learning' 카테고리의 다른 글

티스토리툴바