Linear Algebra
Linear Algebra (선형대수학)은 벡터 공간, 행렬, 선형 변환 등의 개념을 연구하는 수학의 한 분야입니다
- 주로 다차원 공간에서의 벡터와 행렬의 연산 및 이들 간의 관계를 다루며, 공학, 물리학, 컴퓨터 과학 등 다양한 분야에서 중요한 역할을 합니다.
- 또한 많은 데이터 과학 개념과 기술을 뒷받침합니다.
import re, math, random # regexes, math functions, random numbers
import matplotlib.pyplot as plt # pyplot
from collections import defaultdict, Counter
from functools import partial, reduce
Vectors
Vectors는 어떤 finite-dimensional 공간에 있는 점입니다.
- 데이터를 벡터로 생각합니다
- numeric(숫자) 데이터를 나타내는 좋은 방법 입니다.
- 3차원 벡터(키, 몸무게, 나이)
- 4차원 벡터로서의 학생성적(시험1, 시험2, 시험3, 시험4)
- 3차원 공간의 벡터에 해당하는 3개의 숫자 목록
height_weight_age = [70, # inches,
170, # pounds,
40 ] # years
grades = [95, # exam1
80, # exam2
75, # exam3
62 ] # exam4
Vector에 관한 Arithmetic(산술)
벡터 연산을 정의합니다
- 이 파이썬 코드들을 설명을 위한 수학적 정의로 상상해 보십시오
- 목록의 성능이 형편없습니다
- 대용량 데이터가 있는 실제 애플리케이션에서 numpy Array를 사용해야 합니다.
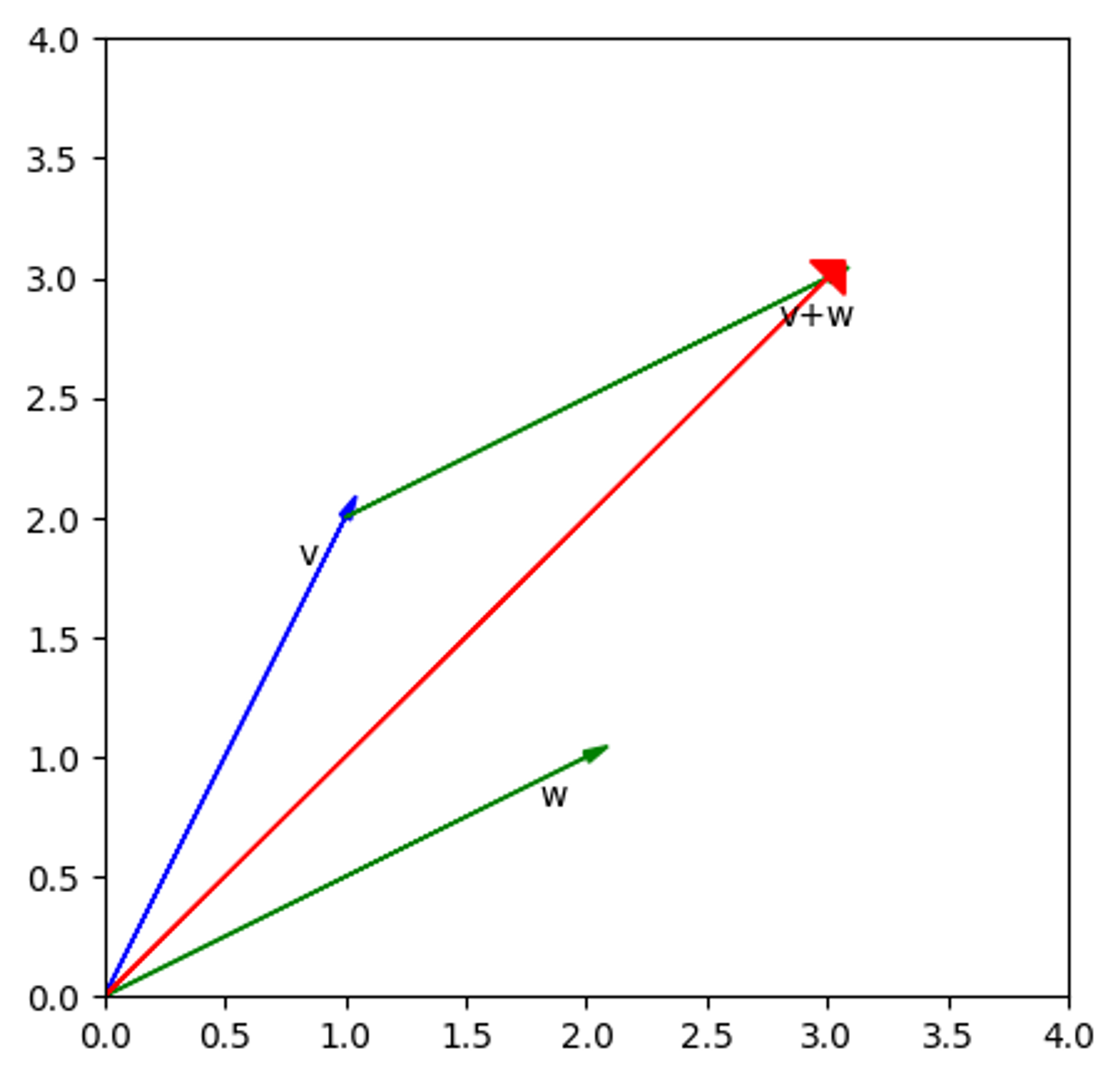
Adding two vectors
# Jupyter Notebook에서 그래프를 인라인 모드로 표시하기 위해 매직 명령어를 사용합니다.
%matplotlib inline
# 필요한 라이브러리 가져오기
import numpy as np # 숫자 연산을 위한 numpy 라이브러리
import matplotlib.pyplot as plt # 그래프 작성을 위한 matplotlib.pyplot
# 5x5 크기의 그래프 생성
plt.figure(figsize=(5, 5))
# x축은 0부터 4까지, y축은 0부터 4까지 설정
plt.axis([0, 4, 0, 4])
# 벡터 v와 w를 배열로 정의
v = np.array([1, 2])
w = np.array([2, 1])
# 벡터 v를 파란색 화살표로 표시
plt.arrow(0, 0, v[0], v[1], head_width=0.05, head_length=0.1, fc='b', ec='b')
# 벡터 w를 녹색 화살표로 표시
plt.arrow(0, 0, w[0], w[1], head_width=0.05, head_length=0.1, fc='g', ec='g')
# 벡터 v + w를 녹색 화살표로 표시
# 시작점은 벡터 v의 끝점이며, 길이는 벡터 w의 값과 동일
plt.arrow(v[0], v[1], w[0], w[1], head_width=0.05, head_length=0.1, fc='g', ec='g')
# 벡터 v + w를 빨간색 화살표로 표시
plt.arrow(0, 0, v[0] + w[0], v[1] + w[1], head_width=0.2, head_length=0.1, fc='r', ec='r')
# 각 벡터의 끝점에 라벨을 추가
offset = np.array([-0.2, -0.2])
plt.annotate('v', xy=v + offset)
plt.annotate('w', xy=w + offset)
plt.annotate('v+w', xy=v + w + offset)
# 그래프 표시
plt.show()
def vector_add(v, w):
"""두 벡터를 요소별로 더해주는 함수
매개변수:
v -- 첫 번째 벡터 (리스트 형태), w -- 두 번째 벡터 (리스트 형태)
반환값:
두 벡터의 각 요소를 더한 결과 벡터 (리스트 형태)
"""
# zip 함수를 사용하여 두 벡터의 요소를 쌍으로 묶습니다.
# 각 요소 쌍 v_i, w_i에 대해 요소별로 더한 값을 리스트로 반환합니다.
return [v_i + w_i for v_i, w_i in zip(v, w)]
def vector_subtract(v, w):
"""두 벡터를 요소별로 빼주는 함수
매개변수:
v -- 첫 번째 벡터 (리스트 형태) w -- 두 번째 벡터 (리스트 형태)
반환값:
두 벡터의 각 요소를 뺀 결과 벡터 (리스트 형태)
"""
# zip 함수를 사용하여 두 벡터의 요소를 쌍으로 묶습니다.
# 각 요소 쌍 v_i, w_i에 대해 요소별로 빼는 값을 리스트로 반환합니다.
return [v_i - w_i for v_i, w_i in zip(v, w)]
def vector_sum(vectors):
"""벡터의 리스트를 입력받아 모든 벡터의 요소별 합을 계산하는 함수
매개변수:
vectors -- 벡터의 리스트
반환값:
벡터의 요소별 합 (리스트 형태)
"""
# functools.reduce 함수를 사용하여 `vector_add` 함수를 활용해 벡터를 요소별로 합합니다.
return reduce(vector_add, vectors)
def scalar_multiply(c, v):
"""스칼라와 벡터의 요소별 곱을 계산하는 함수
매개변수:
c -- 스칼라 (숫자형), v -- 벡터 (리스트 형태)
반환값:
스칼라 c와 벡터 v의 각 요소를 곱한 결과 벡터 (리스트 형태)
"""
# 벡터 v의 각 요소 v_i에 스칼라 c를 곱하여 리스트로 반환합니다.
return [c * v_i for v_i in v]
def vector_mean(vectors):
"""입력 벡터의 i번째 요소의 평균을 계산하여 새로운 벡터를 생성하는 함수
매개변수:
vectors -- 벡터의 리스트
반환값:
각 벡터의 요소별 평균을 계산하여 얻은 새로운 벡터 (리스트 형태)
"""
n = len(vectors) # 벡터의 리스트에 있는 벡터의 수
# 벡터들의 요소별 평균을 계산하기 위해 먼저 벡터의 합을 구하고,
# 스칼라 1/n을 곱하여 평균을 구합니다.
return scalar_multiply(1/n, vector_sum(vectors))
Numpy Version
# numpy 버전의 벡터 연산 함수
import numpy as np
# 세 개의 벡터를 정의합니다.
u = np.array([1,1,1])
v = np.array([1,0,0])
w = np.array([0,1,0])
print(v + w) # 벡터 v와 w를 더합니다.
print(v - w) # 벡터 v에서 w를 뺍니다.
vs = np.array([u, v, w]) # u, v, w 세 개의 벡터를 묶은 배열을 만듭니다.
print(np.sum(vs, axis=0)) # vs 배열의 각 열의 합을 계산합니다.
# axis=0을 사용하면 각 벡터의 요소를 합쳐서 하나의 벡터로 반환합니다.
print(10 * v) # 벡터 v에 스칼라 10을 곱합니다.
print(np.mean(vs, axis=0)) # vs 배열의 각 열의 평균을 계산합니다.
# axis=0을 사용하면 각 벡터의 요소를 합쳐서 하나의 벡터로 반환합니다.
[1 1 0]
[ 1 -1 0]
[2 2 1]
[10 0 0]
[0.66666667 0.66666667 0.33333333]
def dot(v, w):
"""v_1 * w_1 + ... + v_n * w_n 형태의 내적을 계산합니다."""
return sum(v_i * w_i for v_i, w_i in zip(v, w))
def sum_of_squares(v):
"""v_1 * v_1 + ... + v_n * v_n 형태의 제곱합을 계산합니다."""
return dot(v, v)
def magnitude(v):
"""벡터의 제곱합을 계산한 후 제곱근을 구합니다."""
return math.sqrt(sum_of_squares(v))
- dot(v, w) 함수는 두 벡터 v와 w의 내적을 계산합니다. 각 요소 v_i와 w_i의 곱을 계산한 후 모두 합합니다.
- sum_of_squares(v) 함수는 벡터 v의 제곱합을 계산합니다. 벡터 v와 자신과의 내적을 계산합니다.
- magnitude(v) 함수는 벡터 v의 크기를 계산합니다.
- sum_of_squares(v) 함수로 계산한 제곱합의 제곱근을 계산하여 벡터의 크기를 구합니다.
v = np.array([1,0,0]) # 벡터 v를 정의합니다.
w = np.array([0,1,0]) # 벡터 w를 정의합니다.
print(np.dot(v,w)) # 벡터 v와 w의 내적
print(v.dot(w)) # 벡터 v와 w의 내적
print(np.dot(v,v)) # 벡터 v의 제곱합
print(np.sqrt(np.dot(v,v))) # 벡터 v의 크기
print(np.linalg.norm(v)) # 벡터 v의 크기
0
0
1
1.0
1.0
- np.dot(v, w)와 v.dot(w)는 벡터 v와 w의 내적을 계산합니다. 두 벡터는 직교하므로 결과는 0입니다.
- np.dot(v, v)는 벡터 v의 각 요소를 제곱한 후 더하여 벡터 v의 제곱합을 계산합니다. 결과는 1입니다.
- np.sqrt(np.dot(v, v))는 벡터 v의 제곱합을 계산한 후, 제곱근을 구하여 벡터 v의 크기를 계산합니다. 결과는 1.0입니다.
- np.linalg.norm(v)는 np.linalg.norm() 함수를 사용하여 벡터 v의 크기를 계산합니다.
- 결과는 1.0으로 np.sqrt(np.dot(v, v))의 결과와 동일합니다.
Vector Projection으로 Dot Product(점 곱)

설명 → 𝐯's projection on 𝐰: 𝐯1
- v1 = v⋅w / |w|² * w:
- v1: 벡터 v의 벡터 w에 대한 투영 벡터입니다. 즉, v가 벡터 w와 같은 방향으로 투영된 벡터입니다.
- v⋅w: 벡터 v와 w의 내적(dot product)입니다. 이는 두 벡터 사이의 각도에 따라 크기를 계산합니다.
- |w|²: 벡터 w의 크기(절대값)인 |w|의 제곱입니다.
- w: 벡터 w 자체입니다.
- 위 식은 벡터 v의 벡터 w에 대한 투영을 계산합니다. 투영된 벡터 v1는 벡터 w와 같은 방향의 벡터이며, 크기는 v⋅w / |w|²입니다.
- 식의 작동 방식은 다음과 같습니다:
- v와 w의 내적을 계산하여 두 벡터 사이의 관계를 측정합니다. 이는 벡터 v가 벡터 w와 어느 정도 방향이 같은지를 나타냅니다.
- 이 값을 벡터 w의 크기의 제곱(즉, |w|²)으로 나누어 정규화합니다.
- 이 값에 벡터 w를 곱하여 벡터 v1를 계산합니다.
def squared_distance(v, w):
"""두 벡터 v와 w 사이의 제곱 거리(squared distance)를 계산합니다."""
return sum_of_squares(vector_subtract(v, w))
- vector_subtract(v, w)는 벡터 v에서 벡터 w를 뺀 결과를 반환하는 함수입니다.
- sum_of_squares(vector_subtract(v, w))는 위의 결과 벡터의 각 요소를 제곱하고 모두 합한 값을 반환합니다.
- 이를 통해 두 벡터 사이의 제곱 거리를 계산합니다.
Euclidean Distance between two vectors
설명 → Euclidean Distance between two vectors: 𝐩,𝐪
- 벡터 p와 q가 각각 다음과 같은 좌표를 가진다고 가정합니다.
- p = [p1,p2,...,pn]
- [𝑝1,𝑝2,...,𝑝𝑛]
- q = [q1,q2,...,qn]
- [𝑞1,𝑞2,...,𝑞𝑛]
- 이 때, p와 q 사이의 유클리드 거리는 다음과 같이 계산할 수 있습니다:
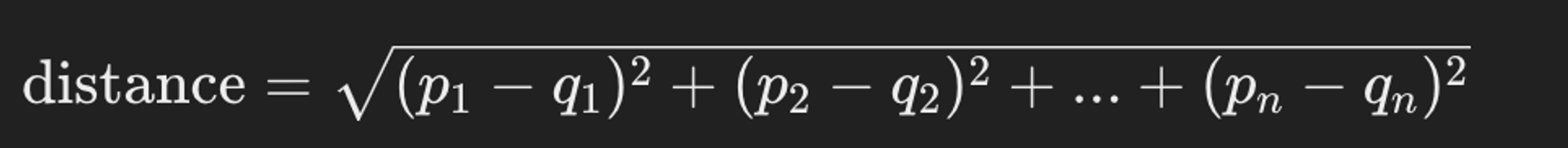
- 이는 두 벡터 사이의 각 좌표 차이의 제곱을 모두 더한 후, 그 값의 제곱근을 취한 것입니다.
- 다른 표현으로, 두 벡터 사이의 유클리드 거리는 두 벡터 p와 q의 차이 벡터를 구한 후, 그 차이 벡터의 크기를 계산한 값이라고도 볼 수 있습니다.
- distance = ∥𝑝−𝑞∥
def distance(v, w):
"""두 벡터 v와 w 사이의 유클리드 거리를 계산합니다."""
return math.sqrt(squared_distance(v, w))
- squared_distance(v, w) 함수는 v와 w 사이의 제곱 거리를 계산합니다.
- math.sqrt는 위에서 계산된 제곱 거리를 제곱근을 구하여 유클리드 거리를 반환합니다.
- 이 함수를 사용하여 두 벡터 사이의 거리를 측정할 수 있습니다.
Manhattan distance
맨해튼 거리(Manhattan distance)는 두 벡터 또는 두 점 사이의 거리를 계산하는 방법 중 하나입니다.
- 거리는 각 좌표 차이의 절대값을 합하여 계산합니다. 맨해튼 거리는 직선으로만 이동할 수 있는 도심(Manhattan) 거리에서 비롯된 이름으로, 축방향 거리(axis-aligned distance)라고도 합니다.
- 두 벡터 p와 q가 다음과 같은 좌표를 가진다고 가정합니다:
- p = [p1,p2,...,pn]
- [𝑝1,𝑝2,...,𝑝𝑛]
- q = [q1,q2,...,qn]
- [𝑞1,𝑞2,...,𝑞𝑛]
- 이 때, p와 q 사이의 맨해튼 거리는 다음과 같이 계산할 수 있습니다:
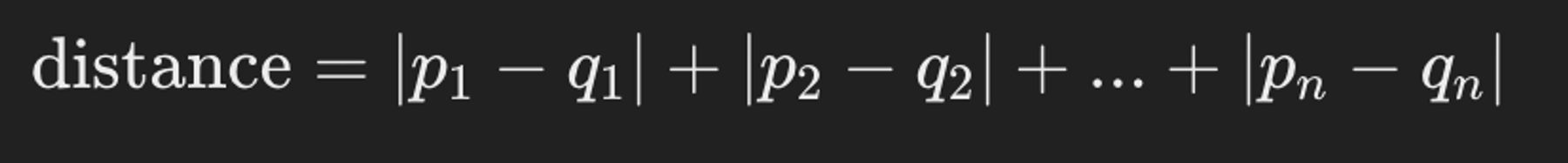
- 이는 두 벡터 사이의 각 좌표 차이의 절대값을 모두 합한 것입니다.
def manhattan_distance(v, w):
"""두 벡터 v와 w 사이의 맨해튼 거리를 계산합니다."""
return sum(math.fabs(v_i - w_i) for v_i, w_i in zip(v, w))
- zip(v, w)를 사용하여 두 벡터 v와 w의 요소를 쌍으로 짝지어 순회합니다.
- v_i와 w_i의 절대값 차이를 계산하고, 이러한 차이들의 합을 반환합니다.
- 맨해튼 거리는 각 차원에서 두 벡터 사이의 절대 차이의 합을 의미합니다.
- 이 함수를 사용하여 두 벡터 사이의 맨해튼 거리를 측정할 수 있습니다.
Cosine similarity
코사인 유사도(Cosine similarity)는 두 벡터 사이의 방향성을 비교하는 척도입니다.
- 이 척도는 두 벡터 사이의 코사인 각도(cosine of the angle)를 사용하여 두 벡터의 유사도를 측정합니다.
- 유사도는 두 벡터가 서로 얼마나 비슷한 방향을 가지고 있는지 나타내며, -1에서 1 사이의 값을 가집니다.
- 코사인 유사도는 다음과 같이 계산할 수 있습니다.

- v⋅w: 벡터 v와 w의 내적(dot product)입니다. 이는 두 벡터의 각 좌표를 곱한 후 모두 더한 값입니다.
- ∥𝑣∥∥v∥와 ∥𝑤∥: 각각 벡터 v와 w의 크기(절대값)입니다. 벡터의 크기는 각 좌표의 제곱합의 제곱근으로 계산합니다.
- 분모는 두 벡터의 크기를 곱한 값이며, 분자는 두 벡터의 내적입니다.
코사인 유사도는 -1에서 1 사이의 값을 가집니다.
1: 두 벡터가 완전히 같은 방향을 가지고 있습니다.
0: 두 벡터가 수직(직각) 방향입니다.
-1: 두 벡터가 완전히 반대 방향입니다.
def cosine_similarity(v, w):
"""두 벡터 v와 w 사이의 코사인 유사도를 계산합니다."""
return dot(v, w) / (magnitude(v) * magnitude(w))
v = [0,1,1,0]
w = [0,100,100,0]
u = [1,0,0,1]
y = [-1,0,0,-1]
print(cosine_similarity(v, w))
print(cosine_similarity(u, v))
print(cosine_similarity(u,y)
0.9999999999999999
0.0
-0.9999999999999998
- dot(v, w)는 v와 w의 내적을 계산합니다.
- magnitude(v)와 magnitude(w)는 각각 v와 w의 크기를 계산합니다.
- 코사인 유사도는 두 벡터의 내적을 각 벡터의 크기를 곱한 값으로 나눈 값입니다.
- 이 값은 두 벡터의 방향이 얼마나 유사한지(각도가 얼마나 작은지)를 나타냅니다.
- 코사인 유사도의 값은 -1에서 1까지의 범위를 가지며, 1에 가까울수록 두 벡터의 방향이 유사함을 의미합니다.
Numpy Version
import numpy as np
v = np.array([1,1])
w = np.array([10,10])
print(np.dot(v - w, v - w)) # 제곱 거리
print(np.sqrt(np.dot(v - w, v - w))) # 유클리드 거리
print(np.sum(np.fabs(v - w))) # 맨해튼 거리
print(np.dot(v, w) / (np.sqrt(np.dot(v, v)) * np.sqrt(np.dot(w, w)))) # 코사인 유사도
162
12.727922061357855
18.0
0.9999999999999998
- 문서 벡터에서 모든 구성 요소가 음수가 아니므로 코사인 유사도는 0과 1 사이이며 코사인거리는 아래의 코드처럼 표현됩니다.
cosine_distance(v, w) = 1 - cosine_similarity(v, w)
def cosine_distance(v, w):
"""벡터 v와 w 사이의 코사인 거리를 계산합니다."""
return 1 - cosine_similarity(v, w)
Matrics (행렬)
행렬(Matrix)은 수학 및 공학에서 중요한 도구로, 숫자나 변수의 직사각형 배열을 의미합니다.
- 행렬은 다양한 연산과 변환을 표현하는 데 사용되며, 선형 대수학의 핵심 개념 중 하나입니다.
- 행렬을 목록으로 표시합니다
- A가 행렬이면 A[i][j]는 i번째 행과 j번째 열에 있는 원소입니다.
A = [[1, 2, 3],
[4, 5, 6]] # A has 2 rows and 3 columns
B = [[1, 2],
[3, 4],
[5, 6]] # B has 3 rows and 2 columns
- 만약에 1,000명의 키, 몸무게, 그리고 나이의 데이터를 가지고 있다면, 그것을 행렬에 넣을 수 있습니다:
data = [[70, 170, 40],
[65, 120, 26],
[77, 250, 19],
# ....
]
def shape(A):
# 행렬 A의 행과 열 수를 반환
num_rows = len(A)
num_cols = len(A[0]) if A else 0
return num_rows, num_cols
def get_row(A, i):
# 행렬 A의 i번째 행을 반환
return A[i]
def get_column(A, j):
# 행렬 A의 j번째 열을 반환
return [A_i[j] for A_i in A]
def make_matrix(num_rows, num_cols, entry_fn):
# 주어진 크기의 행렬을 생성하고 entry_fn에 따라 채움
return [[entry_fn(i, j) for j in range(num_cols)]
for i in range(num_rows)]
def is_diagonal(i, j):
# 대각선에 해당하는 경우 1, 그 외에는 0을 반환
return 1 if i == j else 0
identity_matrix = make_matrix(5, 5, is_diagonal) # 5x5 항등 행렬 생성
import random
random_matrix = make_matrix(5, 5, lambda i, j: random.choice([0, 1])) # 5x5 랜덤 행렬 생성
random_matrix
[[0, 1, 1, 1, 0],
[0, 0, 1, 0, 1],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[1, 0, 0, 0, 1]]
- shape(A):
- 역할: 행렬 A의 행과 열의 수를 반환합니다.
- 사용: 행렬의 크기를 알고 싶을 때 사용합니다.
- get_row(A, i):
- 역할: 행렬 A의 i번째 행을 반환합니다.
- 사용: 행렬의 특정 행을 추출하고자 할 때 사용합니다.
- get_column(A, j):
- 역할: 행렬 A의 j번째 열을 반환합니다.
- 사용: 행렬의 특정 열을 추출하고자 할 때 사용합니다.
- make_matrix(num_rows, num_cols, entry_fn):
- 역할: num_rows x num_cols 크기의 행렬을 생성합니다. 행렬의 각 요소는 entry_fn 함수에 의해 채워집니다.
- 사용: 주어진 크기의 행렬을 특정한 규칙에 따라 생성하고자 할 때 사용합니다.
- is_diagonal(i, j):
- 역할: 인덱스 i와 j가 같은 경우 1을 반환하고, 다르면 0을 반환합니다. 대각선에 있는지를 확인합니다.
- 사용: 행렬의 대각선 부분을 채우는 데 사용됩니다.
- identity_matrix:
- 역할: make_matrix 함수를 이용하여 5x5 크기의 항등 행렬을 생성합니다.
- 사용: 항등 행렬을 생성하고자 할 때 사용됩니다.
- random_matrix:
- 역할: make_matrix 함수를 이용하여 5x5 크기의 랜덤 행렬을 생성합니다. 각 요소는 0 또는 1로 무작위로 채워집니다.
- 사용: 랜덤 행렬을 생성하고자 할 때 사용됩니다.
Numpy Version
A = np.array([[1, 2, 3],
[4, 5, 6]])
B = np.array([[1, 2],
[3, 4],
[5, 6]])
A.shape # 행과 열의 개수를 나타냅니다.
A[1, :] # 행 1의 모든 열 요소를 가져옵니다.
A[:, 1] # 열 1의 모든 행 요소를 가져옵니다.
np.eye(5, 5) # 5x5 단위행렬을 생성합니다.
# 5x5 크기의 행렬을 [0,1] 중에서 무작위로 선택하여 생성합니다.
np.array([np.random.choice([0, 1]) for _ in np.arange(25)]).reshape(5, 5)
# 5x5 크기의 행렬을 무작위로 생성하고, 각 요소를 0.5 이상인지를 판단하여 0 또는 1로 변환합니다.
np.vectorize(np.int)(np.random.rand(25) >= 0.5).reshape(5, 5)
array([[1, 1, 0, 0, 0],
[0, 0, 1, 0, 1],
[1, 1, 0, 0, 0],
[0, 0, 1, 1, 0],
[1, 0, 0, 1, 1]])
- dot(v, w)는 v와 w의 내적을 계산합니다.
- magnitude(v)와 magnitude(w)는 각각 v와 w의 크기를 계산합니다.
- 코사인 유사도는 두 벡터의 내적을 각 벡터의 크기를 곱한 값으로 나눈 값입니다.
- 이 값은 두 벡터의 방향이 얼마나 유사한지(각도가 얼마나 작은지)를 나타냅니다.
- 코사인 유사도의 값은 -1에서 1까지의 범위를 가지며, 1에 가까울수록 두 벡터의 방향이 유사함을 의미합니다.
Two representations for friendships
- representation in Chapter 1
friendships = [(0, 1), (0, 2), (1, 2), (1, 3), (2, 3), (3, 4),
(4, 5), (5, 6), (5, 7), (6, 8), (7, 8), (8, 9)]
- Alternative notation
# user 0 1 2 3 4 5 6 7 8 9
#
friendships = [[0, 1, 1, 0, 0, 0, 0, 0, 0, 0], # user 0
[1, 0, 1, 1, 0, 0, 0, 0, 0, 0], # user 1
[1, 1, 0, 1, 0, 0, 0, 0, 0, 0], # user 2
[0, 1, 1, 0, 1, 0, 0, 0, 0, 0], # user 3
[0, 0, 0, 1, 0, 1, 0, 0, 0, 0], # user 4
[0, 0, 0, 0, 1, 0, 1, 1, 0, 0], # user 5
[0, 0, 0, 0, 0, 1, 0, 0, 1, 0], # user 6
[0, 0, 0, 0, 0, 1, 0, 0, 1, 0], # user 7
[0, 0, 0, 0, 0, 0, 1, 1, 0, 1], # user 8
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0]] # user 9
friendships[0][2] == 1 # True, 0과 2는 친구입니다
friendships[0][8] == 1 # False, 0, 8은 친구가 아닙니다
False
friends_of_five = [i # only need
for i, is_friend in enumerate(friendships[5]) # to look at
if is_friend] # one row
print(friends_of_five)
[4, 6, 7]
Numpy Version
friendships = np.array(friendships) # 친구 관계를 나타내는 2D 배열을 만듭니다.
# 0과 2가 친구인지 확인합니다. (0행, 2열 값이 1이면 True)
print(friendships[0, 2] == 1)
# 0과 8이 친구인지 확인합니다. (0행, 8열 값이 1이면 True)
print(friendships[0, 8] == 1)
# 5의 친구 목록을 가져옵니다. (5행의 값 중 1인 요소들의 인덱스를 반환합니다.)
print(np.argwhere(friendships[5] == 1))
array([[4],
[6],
[7]], dtype=int64)
Matrix Addition
def matrix_add(A, B):
# 두 행렬의 크기가 다른 경우 예외를 발생시킵니다.
if shape(A) != shape(B):
raise ArithmeticError("cannot add matrices with different shapes")
# 행렬 A와 B의 크기를 가져옵니다.
num_rows, num_cols = shape(A)
# 각 위치의 요소들을 더하여 새로운 행렬을 생성합니다.
def entry_fn(i, j): return A[i][j] + B[i][j]
# `make_matrix` 함수를 사용하여 결과 행렬을 생성합니다.
return make_matrix(num_rows, num_cols, entry_fn)
- shape(A) != shape(B): 행렬 A와 B의 크기를 비교합니다. 크기가 다르면 예외를 발생시킵니다.
- num_rows, num_cols = shape(A): 행렬 A의 행과 열의 수를 가져옵니다.
- def entry_fn(i, j): return A[i][j] + B[i][j]: 각 위치 (i, j)에서 A와 B의 요소를 더하는 함수입니다.
- return make_matrix(num_rows, num_cols, entry_fn): make_matrix 함수를 사용하여 결과 행렬을 생성합니다.
Numpy Version
A = np.array([[1,1],[2,2]])
B = np.array([[3,3],[4,4]])
print(A + B) # 행렬 A와 B의 요소별 덧셈 (원소별 덧셈)
print(A * B) # 행렬 A와 B의 요소별 곱셈 (원소별 곱셈)
print(np.transpose(A)) # 행렬 A의 전치 (행과 열을 뒤집은 형태)
print(A.T) # 행렬 A의 전치 (np.transpose(A)와 동일)
print(A.dot(B)) # 행렬 A와 B의 행렬 곱셈
print(np.matmul(A, B)) # 행렬 A와 B의 행렬 곱셈 (A.dot(B)와 동일)
C = np.array([[1., 2.], [3., 4.]])
print(np.linalg.det(C)) # 행렬 C의 행렬식 (determinant)
print(np.linalg.inv(C)) # 행렬 C의 역행렬 (inverse)
print(C.dot(np.linalg.inv(C))) # 행렬 C와 C의 역행렬의 곱셈 (결과는 단위 행렬)
print(np.linalg.eig(C)) # 행렬 C의 고유값과 고유벡터 (eigenvalues and eigenvectors)
[[4 4]
[6 6]]
[[3 3]
[8 8]]
[[1 2]
[1 2]]
[[1 2]
[1 2]]
[[ 7 7]
[14 14]]
[[ 7 7]
[14 14]]
-2.0000000000000004
[[-2. 1. ]
[ 1.5 -0.5]]
[[1.00000000e+00 1.11022302e-16]
[0.00000000e+00 1.00000000e+00]]
(array([-0.37228132, 5.37228132]), array([[-0.82456484, -0.41597356],
[ 0.56576746, -0.90937671]]))
More on types of attributes
- 명목(Nominal) 속성:
- 속성 값 간에 우선순위나 순위가 없습니다. 즉, 모든 값은 동등합니다.
- 예: ID 번호, 눈 색깔, 우편번호 등. 이들은 서로 구별되지만 순위나 크기가 없습니다.
- 서열(Ordinal) 속성:
- 속성 값 간에 우선순위나 순위가 있습니다. 그러나 값 사이의 차이가 일정하지 않습니다.
- 예: 순위 (예: 감자 칩의 맛을 1~10까지 평가), 학년, 키 (예: 키가 큰, 중간, 작은) 등이 있습니다.
- 구간(Interval) 속성:
- 속성 값 간의 차이를 비교할 수 있지만, 절대적인 영점(0)이 없습니다.
- 예: 달력 날짜, 섭씨나 화씨 온도 등. 온도의 경우 차이는 비교할 수 있지만, 섭씨나 화씨는 절대적인 영점이 없습니다.
- 비율(Ratio) 속성:
- 절대적인 영점(0)이 있으며 속성 값 간의 비율을 비교할 수 있습니다.
- 예: 켈빈 온도, 길이, 시간, 개수 등. 이러한 속성은 0이 의미 있는 값을 가지므로 값 간의 비율을 비교할 수 있습니다.
Properties of Attribute Values
- 속성의 유형은 다음 속성/작업 중 어느 것을 소유하는지에 따라 달라집니다.
- 구별성(Distinctness): =
- 속성 값이 서로 다른지 여부를 확인하는 연산입니다. 속성 값 사이에 구별성이 있다면 해당 속성은 서로 다른 값을 가질 수 있습니다. 이는 명목(Nominal), 서열(Ordinal), 구간(Interval), 비율(Ratio) 속성 모두에 해당됩니다.
- 순서(Order): < >
- 속성 값 간의 순서를 비교하는 연산입니다. 예를 들어, 어느 값이 다른 값보다 작은지, 큰지 등을 비교할 수 있습니다. 이는 서열(Ordinal), 구간(Interval), 비율(Ratio) 속성에 해당합니다.
- 차이(Differences): + -
- 속성 값 간의 차이를 계산할 수 있는 연산입니다. 예를 들어, 속성 값 사이의 차이를 계산하여 의미 있는 정보를 얻을 수 있습니다. 이는 구간(Interval), 비율(Ratio) 속성에 해당합니다.
- 비율(Ratios): * /
- 속성 값 간의 비율을 계산할 수 있는 연산입니다. 예를 들어, 한 속성 값이 다른 속성 값의 몇 배인지를 계산할 수 있습니다. 이는 비율(Ratio) 속성에 해당합니다.
각 속성 유형은 이러한 속성/연산 중 일부 또는 모든 것을 갖고 있습니다.
- 명목(Nominal) 속성: 구별성(Distinctness)
- 서열(Ordinal) 속성: 구별성(Distinctness)과 순서(Order)
- 구간(Interval) 속성: 구별성(Distinctness), 순서(Order), 의미 있는 차이(Differences)
- 비율(Ratio) 속성: 구별성(Distinctness), 순서(Order), 의미 있는 차이(Differences), 비율(Ratios)
'📈 Data Engineering > 📝 Data Mining' 카테고리의 다른 글
| [Data Mining] Gradient Descent (경사 하강법) (0) | 2024.07.23 |
|---|---|
| [Data Mining] Statistics (통계학) (0) | 2024.07.14 |
| [Data Mining] Introduction to Numpy part.2 (0) | 2024.07.05 |
| [Data Mining] Introduction to Numpy part.1 (0) | 2024.06.26 |
| [Data Mining] Visualizing Data (0) | 2024.06.25 |