이번에는 Linear Regression (선형회귀)에 데하여 알아보겠습니다.
Linear Regression (선형회귀)
선형 회귀(Linear Regression)는 머신러닝에서 널리 사용되는 회귀 분석 기법 중 하나로,
독립 변수와 종속 변수 간의 관계를 선형 방정식으로 표현합니다.
- 이 방법은 주어진 데이터를 이용해 가장 잘 맞는 직선을 찾는 것이 목표입니다.
- 선형 회귀는 모델이 비교적 간단하고 해석이 용이하다는 장점이 있습니다.
회귀 방정식
선형 회귀 모델은 다음과 같은 형태의 방정식을 사용합니다.
Y = β0 +β1X + ϵ
- : 종속 변수 (예측하려는 값)
- X: 독립 변수 (설명 변수)
- β0: 절편 (Intercept)
- β1: 기울기 (Slope)
- ϵ: 오차 항 (Error Term, 모델의 예측과 실제 값 간의 차이)
- 모델의 목표는 주어진 데이터에 가장 잘 맞는 β0(절편)와 β1(기울기)를 찾는 것입니다
- 즉, 독립 변수 X와 종속 변수 Y 간의 관계를 가장 잘 설명하는 선형 방정식을 찾는 것이 목적입니다.
잔차 제곱합 최소화 (Ordinary Least Squares, OLS)
최적의 직선을 찾기 위해, OLS 방법을 사용합니다.
- 이 방법은 잔차의 제곱합을 최소화하는 를 찾는 것을 목표로 합니다.
- 잔차(Residual)란 실제 값과 예측 값의 차이를 의미하며, 이를 제곱한 후 합산한 것이 잔차 제곱합(RSS)입니다.
- 잔차 제곱합 RSS는 아래와 같이 정의됩니다.

- : 데이터 포인트의 총 개수
- yi: i번째 데이터 포인트의 실제 값
- xi: i번째 데이터 포인트의 독립 변수 값
- : 회귀 모델의 절편 (Intercept)
- : 회귀 모델의 기울기 (Slope)
- β0 + β1xi + : i번째 데이터 포인트에 대한 예측 값
OLS는 이 잔차 제곱합 RSS를 최소화하는 와 찾는 방법입니다.
단순 선형 회귀 (Simple Linear Regression)
단순 선형 회귀는 하나의 독립 변수와 하나의 종속 변수 간의 관계를 모델링합니다.
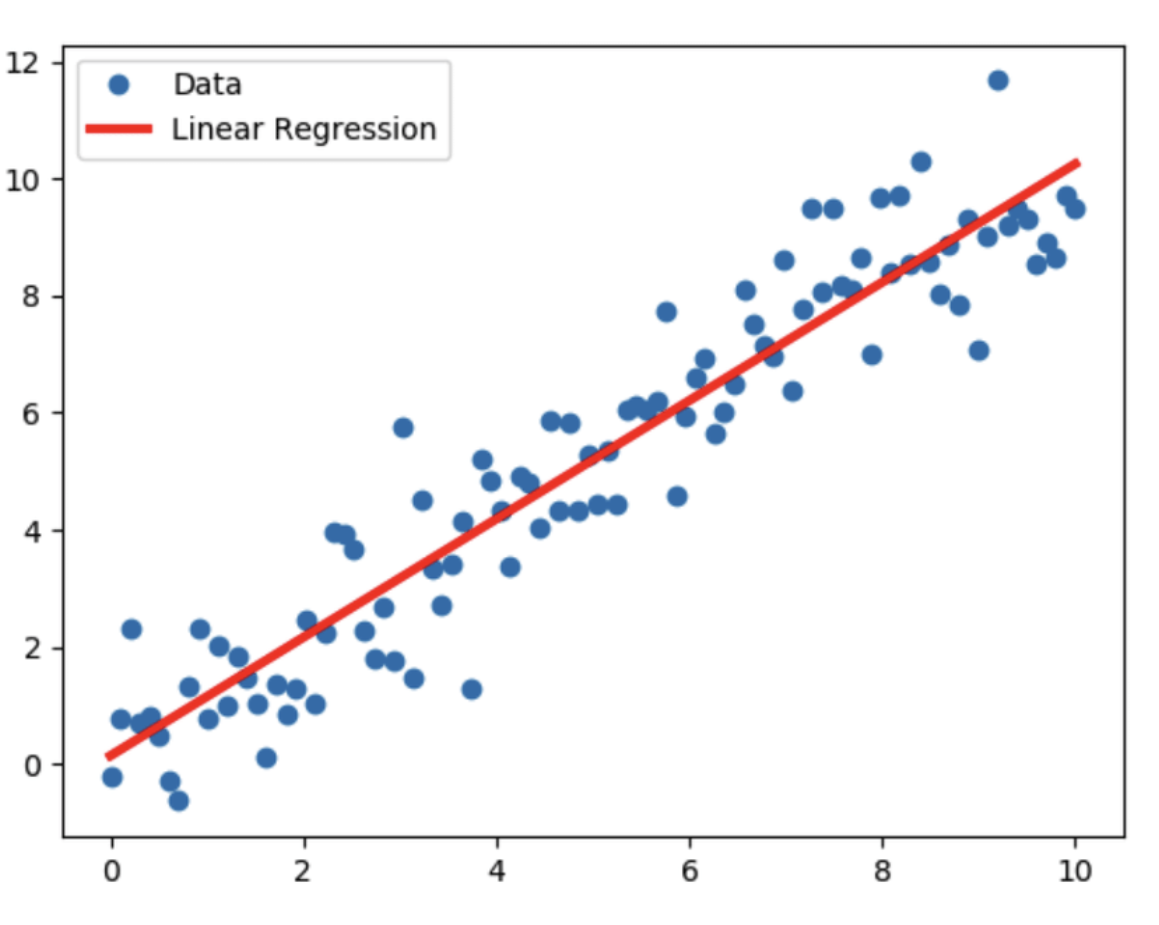
- 예를 들어, 주택의 크기(독립 변수)와 주택의 가격(종속 변수) 간의 관계를 분석하는 것입니다.
- 이 경우, 회귀 방정식은 다음과 같은 형태입니다.
y = β0 + β1x
- 예: 주택 크기 x에 따른 주택 가격 y를 모델링 하는 것입니다.
다중 선형 회귀 (Multiple Linear Regression)
다중 선형 회귀는 여러 개의 독립 변수를 사용하여 종속 변수를 예측합니다.
- 이 경우, 여러 독립 변수가 종속 변수에 미치는 영향을 동시에 고려할 수 있습니다. 회귀 방정식은 다음과 같이 표현됩니다.
y = β0 + β1x1 + β2x2 + ⋯ + βkxk
- x1,x2,…,xk: 여러 독립 변수들
- β1,β2,…,βk: 각 독립 변수에 대한 계수들
- 예: 주택 가격(y)을 예측할 때, 주택 크기(x1), 방 개수(x2), 위치(x3) 등의 여러 독립 변수를 고려할 수 있습니다.
모델 적합성 평가
R-제곱 (R-squared)
R-제곱은 모델이 데이터를 얼마나 잘 설명하는지를 나타내는 지표입니다.
- 0과 1 사이의 값을 가지며, 1에 가까울수록 모델이 데이터를 잘 설명한다는 의미입니다.
- R-제곱은 다음과 같이 계산됩니다.

- 여기서
- : 실제 값
- y^i: 예측 값
- yˉ: 실제 값의 평균
- n: 데이터 포인트의 총 개수
- 이 수식에서 분자 부분은 잔차 제곱합(Residual Sum of Squares, RSS)이고, 분모 부분은 총 제곱합(Total Sum of Squares, TSS)입니다.
- R-제곱은 RSS와 TSS의 비율을 통해 모델의 성능을 평가합니다.
- R^2 값이 1에 가까울수록 모델이 실제 데이터를 잘 설명한다는 것을 의미합니다.
Example Code (Linear Regression & mse, r^2)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score# 데이터 생성
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
print(f"len(X_train): {len(X_train)}")
# len(X_train): 80# 모델 학습
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
# 예측
y_pred = lin_reg.predict(X_test)# 평가
mse = mean_squared_error(y_test, y_pred) # 평균제곱오차
r2 = r2_score(y_test, y_pred) # 결정계수
print(f'Mean Squared Error: {mse}')
print(f'R^2 Score: {r2}')
# Mean Squared Error: 0.9177532469714291
# R^2 Score: 0.6521157503858556# 시각화
plt.scatter(X_test, y_test, color='black', label='Actual Data')
plt.plot(X_test, y_pred, color='blue', linewidth=3, label='Predicted Line')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression')
plt.legend()
plt.show()
잔차 분석 (Residual Analysis)
잔차는 실제 값과 예측 값의 차이를 나타내며, 잔차 분석을 통해 모델의 적합성을 평가할 수 있습니다.
- 잔차가 무작위로 분포한다면, 모델이 데이터를 잘 적합시킨다는 신호입니다.
- 잔차 분석에서 주로 사용되는 도구는 잔차 플롯(Residual Plot)으로, 예측 값에 대한 잔차를 그래프로 표현합니다.
- 이 플롯에서 잔차가 일정한 패턴 없이 무작위로 분포하면 모델이 적합한 것으로 볼 수 있습니다.
- 잔차 분석과 R-제곱 등의 지표는 모델의 성능과 적합성을 평가하는 중요한 도구입니다.
- 이 과정에서 모델이 데이터를 지나치게 복잡하게 설명하려는 과적합(overfitting)이 일어나지 않도록 주의해야 합니다.
'📈 Data Engineering > 📇 Machine Learning' 카테고리의 다른 글
| [ML] Supervised Learning (지도학습) (0) | 2024.08.06 |
|---|---|
| [ML] Model의 학습과 평가 (0) | 2024.08.02 |
| [ML] Naive Bayes (나이브 베이즈) (0) | 2024.08.01 |
| [ML] Supervised Learning (지도학습) (0) | 2024.07.31 |
| [ML] Machine Learning (머신러닝) Intro (0) | 2024.07.28 |